Überlebensfunktion

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst.

Die Überlebensfunktion gibt die Wahrscheinlichkeit an, dass ein spezielles Ereignis (beispielsweise der Tod eines Patienten) nicht vor einem gewissen Zeitpunkt passiert. Sie ist eine spezielle reelle Funktion in der Stochastik (insbesondere der Ereigniszeitanalyse), die eine Ergänzung zum Konzept der Verteilungsfunktion darstellt. Wie auch bei Verteilungsfunktionen kann jeder Überlebensfunktion eine Wahrscheinlichkeitsverteilung zugeordnet werden. Umgekehrt kann jeder Wahrscheinlichkeitsverteilung auf den reellen Zahlen eine Überlebensfunktion zugeordnet werden.

Ihren Namen tragen die Überlebensfunktionen, weil sie bei der Modellierung von Lebensdauern auftreten, beispielsweise von Individuen oder von Bauteilen. Gebe die Wahrscheinlichkeitsverteilung ${\displaystyle F(t)}$ die kumulative Sterbewahrscheinlichkeit einer Spezies an. Dann entspricht die Überlebensfunktion ${\displaystyle S(t)=1-F(t)}$an der Stelle ${\displaystyle t}$ der Wahrscheinlichkeit, dass ein Individuum älter als ${\displaystyle t}$ wird. Es „überlebt“ also den Zeitpunkt ${\displaystyle t}$. Häufig wird die individuelle Überlebensfunktion betrachtet, welche bedingt auf andere Eigenschaften des Individuums ist.

Eine übliche graphische Darstellung für die Überlebenswahrscheinlichkeit gemittelt über alle Individuen einer Population ist die Überlebenskurve.

Definition

Gegeben sei eine Wahrscheinlichkeitsverteilung ${\displaystyle P}$ auf ${\displaystyle \mathbb {R} }$, versehen mit der Borelschen σ-Algebra ${\displaystyle {\mathcal {B}}(\mathbb {R} )}$, oder eine reellwertige Zufallsvariable ${\displaystyle X}$. Dann heißt

${\displaystyle G_{P}(t):=P((t,+\infty ))}$

beziehungsweise

${\displaystyle G_{X}(t):=P(X>t)}$

die Überlebensfunktion von ${\displaystyle P}$ beziehungsweise ${\displaystyle X}$.

Eigenschaften

Kurvendiskussion

Ähnlich wie bei den Verteilungsfunktionen gilt:

• Es ist ${\displaystyle \lim _{t\to -\infty }G(t)=1}$ und ${\displaystyle \lim _{t\to +\infty }G(t)=0}$
• Die Funktion ${\displaystyle G}$ ist monoton fallend
• Die Funktion ${\displaystyle G}$ ist rechtsseitig stetig

Quantile

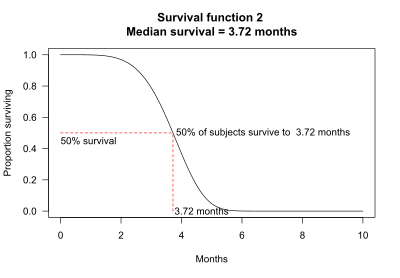
Aus der Überlebensfunktion lassen sich Quantile direkt ablesen. Beispielsweise ist die geschätzte Median-Überlebenszeit der Wert, bei dem die Überlebensfunktion den Wert 0.5 annimmt. Konfidenzintervalle für die geschätzten Quantile lassen sich ebenfalls ableiten.^[1]

Erwartungswert

Die Überlebenszeit T ist eine Zufallsvariable mit ${\displaystyle T\sim f}$, wobei ${\displaystyle f}$ die Wahrscheinlichkeitsdichtefunktion ist. Der Erwartungswert ist ${\displaystyle \mathbb {E} (T)=\int _{0}^{\infty }tf(t)dt}$

Wegen${\displaystyle f(t)=-S'(t)}$ gilt:

${\displaystyle \mathbb {E} (T)=-\int _{0}^{\infty }tS'(t)dt,}$

bzw. durch partielle Integration:

${\displaystyle \mathbb {E} (T)=\int _{0}^{\infty }S(t)dt.}$

Beziehung zur Verteilungsfunktion

Ist ${\displaystyle F_{P}}$ die Verteilungsfunktion einer Wahrscheinlichkeitsverteilung ${\displaystyle P}$ und ${\displaystyle G_{P}}$ die Überlebensfunktion von ${\displaystyle P}$, so gilt

${\displaystyle F_{P}(t)+G_{P}(t)=1}$ für alle ${\displaystyle t\in \mathbb {R} }$.

Ebenso gilt für eine Zufallsvariable ${\displaystyle X}$

${\displaystyle F_{X}(t)+G_{X}(t)=1}$ für alle ${\displaystyle t\in \mathbb {R} }$.

Dies folgt direkt aus den Definitionen der jeweiligen Funktionen und der Normiertheit der Wahrscheinlichkeitsverteilungen. Denn die Verteilungsfunktion ist genau die Wahrscheinlichkeit, einen Wert kleinergleich ${\displaystyle t}$ anzunehmen, die Überlebensfunktion die Wahrscheinlichkeit, einen Wert echt größer als ${\displaystyle t}$ anzunehmen. Somit ist ihre Summe die Wahrscheinlichkeit, irgendeinen Wert anzunehmen und damit eins.

Damit kann aus jeder Überlebensfunktion eine Verteilungsfunktion gewonnen werden. Ebenso kann aus jeder Verteilungsfunktion eine Überlebensfunktion gewonnen werden. Insbesondere lässt sich damit analog zum Vorgehen bei Verteilungsfunktionen jeder Funktion, welche die drei unter „Eigenschaften“ aufgezählten Punkte erfüllt, zur Überlebensfunktion einer eindeutig bestimmten Wahrscheinlichkeitsverteilung erklären (siehe auch Korrespondenzsatz).

Bedingte Überlebenswahrscheinlichkeit und Restlebensdauer

Sieht man eine Wahrscheinlichkeitsverteilung als Wahrscheinlichkeit an, dass ein Individuum stirbt oder ein Bauteil versagt, so ist man häufig an einer Neueinschätzung der Überlebensdauer interessiert. Hat zum Beispiel eine Qualitätskontrolle ergeben, dass ein Bauteil zum Zeitpunkt ${\displaystyle t_{0}}$ noch arbeitet, so wird sich auf der Basis dieser Information die Einschätzung die Wahrscheinlichkeit verändern. Mittels der bedingten Wahrscheinlichkeit erhält man dann für die bedingte Überlebenswahrscheinlichkeit

${\displaystyle P\left(X>t_{0}+t\mid X>t_{0}\right)={\frac {G(t+t_{0})}{G(t_{0})}}={\frac {1-F\left(t_{0}+t\right)}{1-F\left(t_{0}\right)}}}$

und für die Restlebensdauer

${\displaystyle F\left(t+t_{0}\mid t_{0}\right)=P\left(X\leq t+t_{0}\mid X>t_{0}\right)={\frac {F\left(t+t_{0}\right)-F\left(t_{0}\right)}{1-F\left(t_{0}\right)}}}$

Weblinks

• Eric W. Weisstein: Survival Function. In: MathWorld (englisch).

Literatur

• Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9, doi:10.1007/978-3-642-21026-6. 

Einzelnachweise

1. ↑ Machin, D., Cheung, Y. B., Parmar, M. (2006). Survival Analysis: A Practical Approach. Deutschland: Wiley. Seite 36 und folgend Google Books