Schwebung
Als Schwebung bezeichnet man den Effekt, dass die Resultierende der additiven Überlagerung (Superposition) zweier Schwingungen, die sich in ihrer Frequenz nur wenig voneinander unterscheiden, eine periodisch zu- und abnehmende Amplitude aufweist.
Schwebungen treten bei Wellen auf, für die das Superpositionsprinzip gilt, also beispielsweise bei Schallwellen, elektromagnetischen Wellen oder elektrischen Signalströmen. Da sich die Momentanwerte der Ausgangsschwingungen je nach Phasenlage gegenseitig periodisch verstärken bzw. abschwächen, hat die Resultierende eine an- und abschwellende Amplitude. Die Frequenz dieses Wechsels ist umso höher, je größer die Differenz der Ausgangsfrequenzen und ist.
Bei der Schwebung werden, im Gegensatz zu den Verfahren, wie sie bei Mischstufen Anwendung finden, keine neuen Frequenzen erzeugt, und es treten auch keine Frequenzverschiebungen auf.
Frequenz und Periode
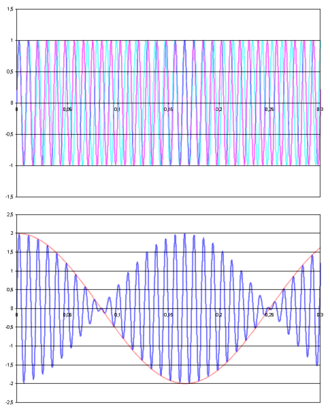
Oben:
Die beiden Signalfrequenzen und in den Farben Cyan und Magenta.
Unten:
Die Schwebung, gebildet durch Addition der beiden obigen Verläufe.
Die Frequenz der blauen Kurve ergibt sich als Mittelwert der beiden Frequenzen; die Frequenz der einhüllenden Kurve (Rot) ergibt sich als die halbe Differenz der beiden Frequenzen.
Zwei harmonische Schwingungen und mit leicht unterschiedlichen Frequenzen und :
Zur Vereinfachung sei angenommen, dass beide Schwingungen dieselbe Amplitude haben.
Dann kann die Summenschwingung (Schwebungsfunktion) so dargestellt werden (Index für Resultierende):
Dieser Ausdruck kann durch Anwendung der trigonometrischen Additionstheoreme umgeformt werden:
Dieser Ausdruck lässt sich vereinfachen mit folgenden Festlegungen:
- : Frequenz der Überlagerungsschwingung (Mittelwert der Einzelfrequenzen)
- : Frequenz der Einhüllenden
Die Schwebungsfrequenz ergibt sich aus dem Verlauf des Betrages der Einhüllenden:
Die Schwebungsperiode
ist der zeitliche Abstand zwischen zwei Punkten minimaler Amplitude (Knoten) der Schwebungsfunktion. Die Schwebungsperiode ist umso größer, je näher die beiden Ausgangsfrequenzen und zusammen liegen.
Sind die Amplituden und der beiden Frequenzen nicht gleich, dann spricht man von einer unreinen Schwebung.
Akustische Schwebungen
In der Akustik ist die Schwebung deutlich zu hören: Erklingen zwei Töne, deren Frequenzen sich nur wenig unterscheiden, so ist ein Ton zu hören, dessen Frequenz dem Mittelwert der Frequenzen der beiden überlagerten Töne entspricht. Dieser Ton ist moduliert, seine Lautstärke schwankt mit der o. g. Schwebungsfrequenz, die der Differenz der Frequenzen der beiden Töne entspricht.
Erhöht sich der Frequenzunterschied, so vermag das Ohr den immer schneller werdenden Lautstärkeschwankungen nicht mehr zu folgen, und man vernimmt einen Ton rauer Klangfärbung, der sich bei weiterer Vergrößerung der Frequenzdifferenz in zwei Einzeltöne aufspaltet. Überschreitet die Schwebungsfrequenz die Hörschwelle von ca. 20 Hz, so wird sie als Differenzton hörbar.
Dieses Phänomen demonstriert das folgende Klangbeispiel: Einem Sinuston mit der konstanten Frequenz 440 Hertz ist ein zweiter Sinuston überlagert, dessen Frequenz von 440 Hertz auf 490 Hertz ansteigt.
Wie die Schwebungen eines Intervalls (hier eines Halbtons) wahrgenommen werden, hängt sehr stark von der Höhenlage ab, was im folgenden Beispiel deutlich wird:
Beispiel: Gespielt werden die (Sinus-)Töne e und f von der großen bis zur dreigestrichenen Oktavlage zuerst einzeln, dann zusammen. Die Frequenz von f ist in jeder Oktavlage um 6,6 % höher als diejenige von e.
| in Hz | E 82,5 | F 88 | E F | e 165 | f 176 | e f | e’ 330 | f’ 352 | e’ f’ | e’’ 660 | f’’ 704 | e’’ f’’ | e’’’ 1320 | f’’’ 1408 | e’’’ f’’’ |
| allein | allein | zusammen | allein | allein | zusammen | allein | allein | zusammen | allein | allein | zusammen | allein | allein | zusammen | |
Klangbeispiele
Schwebungen bei der Überlagerung zweier Töne mit 440 Hz und 440,5 Hz
Mit reinen Sinusschwingungen

Mit 100 % Grundfrequenz, 50 % erster Oberton und 25 % zweiter Oberton

Zwei chromatische Halbtöne (Frequenzunterschied 4 %) im Zusammenklang
 | Reine Sinustöne: Der Schwebungscharakter ist beim Zusammenklang deutlich. Kaum zwei getrennte Töne hörbar.
| Als Orgelregister mit Obertönen (Grundton: 100 %, Obertöne: 75 %, 50 %, 30 %, 15 %, 10 % und 5 %). Hier hört man beim Zusammenklang deutlich zwei getrennte Töne (man kann sie nachsingen).
|
Mit speziellen Schwingungsformen
Um das Verständnis der akustischen Schwebung zu erleichtern, finden sich hier beispielhaft vier Schwingungen, die sich in ihrer Wellenform unterscheiden:
- Dreieckschwingung
- Rechteckschwingung
- Sägezahnschwingung
- Sinusschwingung
In allen vier Klangbeispielen wurden zwei Schwingungen überlagert, die zunächst dieselbe Startfrequenz von 110 Hz haben. Nach 4 Sekunden wird die Frequenz der einen Schwingung allmählich erhöht (in 8 Sekunden um 50 Cent), dann bleibt sie für 6 Sekunden gleich, wird nun rascher als im Anstieg um 100 Cent verringert und nach einer weiteren stabilen Phase bei −50 Cent wieder auf die Ausgangsfrequenz geändert. Den exakten Verlauf stellt folgendes Diagramm dar:

Bei unreinen Intervallen
Bei unrein intonierten Intervallen kann man die Schwebungen der Obertöne folgendermaßen berechnen:
- Oktave:
- Quinte:
Beispiel dazu bei mitteltöniger Stimmung: mitteltönige Quinten
Bei den gewöhnlich außerhalb des kritischen Bereichs liegenden Intervallen hört man eine Schwebung, wenn zwei deutlich vorhandene Obertöne oder ein Oberton und eine Grundfrequenz nahe beieinander liegen.
Wie man den folgenden Wellenbildern entnehmen kann, ist bei reinen Sinustönen kaum eine Schwebung wahrnehmbar (die Amplituden ändert sich kaum), bei einem hohen Obertonanteil ist sie jedoch deutlich hörbar:
Beispiel: mitteltönige Quinte. Zuerst reine Sinusschwingungen, dann mit Obertönen

Schwebungen bei Intervallen spielen bei der reinen, den mitteltönigen, den wohltemperierten und der gleichstufigen Stimmung eine große Rolle. Zum Beispiel hört man bei einer reinen Terz keine, bei der gleichstufigen jedoch eine erhebliche – als Reibung empfundene – Schwebung. Die Schwebungen der mitteltönig gestimmten Quinten sind so gering, dass sie nicht als Missklang empfunden werden.
Akustische Täuschung?
Die auditive Wahrnehmung von Schwebungen beruht im Allgemeinen nicht auf einer akustischen Täuschung, sondern auf realen physikalischen Vorgängen. Anders ist dies bei den binauralen Beats, wo den Ohren über Kopfhörer je eine von zwei differierenden Frequenzen zugeführt wird und die Wahrnehmung von Schwebungen erst durch die Signalverarbeitung im Gehirn entsteht.
Anwendungen
Das Phänomen der Schwebung kann vielseitig angewendet werden, z. B. in der Musizierpraxis:
- Das Stimmen eines Musikinstruments nach Gehör (ohne Stimmgerät mit optischer Anzeige), also das eigentliche Einstimmen auf den Kammerton als Referenzfrequenz, erfolgt solange, bis keine Schwebung mehr zu hören ist: der Ton ist dann „schwebungsnull – er stimmt“.
- Die Schwebung wird als belebender Klangeffekt bei Musikinstrumenten eingesetzt, beispielsweise als zuschaltbarer Tremoloeffekt oder als spezielles Register in Pfeifenorgeln.
- Bei der Tremoloharmonika (Wiener Stimmung) und den meisten Handzuginstrumenten erfolgt die Tonerzeugung mit zwei Durchschlagzungen, die in einer Schwebung gestimmt sind.
- Die Tonharmonie des Bambus-Instruments Angklung basiert auf dem Prinzip von zwei bis vier in Schwebung befindlichen Klangkörpern (Bässe, Melodieinstrumente und Akkorde), die gleichzeitig geschüttelt werden.
- Das Leslie-Lautsprecher-Kabinett verwendet den Doppler-Effekt zur Erzeugung periodisch schwankender Frequenzen. Bei der Überlagerung mit dem Originalton entsteht eine Schwebung.
In der Metrologie wird durch Überlagern von Laserlicht einer nur ungefähr bekannten Frequenz mit einem Frequenzkamm eine elektronisch messbare Schwebung erzeugt, die eine wesentlich genauere Bestimmung der Frequenz des Lasers ermöglicht.
Unangenehm störend wird die Schwebung, wenn zwei Instrumente mit annähernd sinusförmigen Tönen (z. B. Flöten) eng benachbarte Töne spielen – man sagt, die Töne „reiben sich“. Beim Unisono-Spiel zweier Blockflötenanfänger kann es bei extremen Unsauberkeiten sogar dazu kommen, dass in der Tiefe ein äußerst penetranter Differenzton hörbar wird.
Literatur
- Dieter Meschede (Hrsg.): Gerthsen Physik. 22., vollst. neubearb. Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-02622-3.
Weblinks
- Simulation zu Interferenz/Schwebung/Lissajous_Kurven zweier stehender Wellen
































