Continuous Bernoulli distribution

Continuous Bernoulli distribution

Probability density function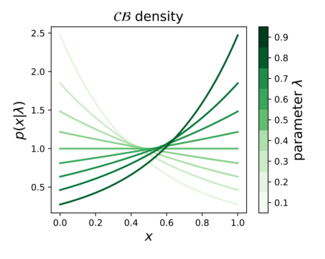
Notation	${\displaystyle {\mathcal {CB}}(\lambda )}$
Parameters	${\displaystyle \lambda \in (0,1)}$
Support	${\displaystyle x\in [0,1]}$
PDF	${\displaystyle C(\lambda )\lambda ^{x}(1-\lambda )^{1-x}\!}$ where ${\displaystyle C(\lambda )={\begin{cases}2&{\text{if }}\lambda ={\frac {1}{2}}\\{\frac {2\tanh ^{-1}(1-2\lambda )}{1-2\lambda }}&{\text{ otherwise}}\end{cases}}}$
CDF	${\displaystyle {\begin{cases}x&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda ^{x}(1-\lambda )^{1-x}+\lambda -1}{2\lambda -1}}&{\text{ otherwise}}\end{cases}}\!}$
Mean	${\displaystyle \operatorname {E} [X]={\begin{cases}{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+{\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ otherwise}}\end{cases}}\!}$
Variance	${\displaystyle \operatorname {var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\-{\frac {(1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2}}}&{\text{ otherwise}}\end{cases}}\!}$

In probability theory, statistics, and machine learning, the continuous Bernoulli distribution^[1][2][3] is a family of continuous probability distributions parameterized by a single shape parameter ${\displaystyle \lambda \in (0,1)}$, defined on the unit interval ${\displaystyle x\in [0,1]}$, by:

${\displaystyle p(x|\lambda )\propto \lambda ^{x}(1-\lambda )^{1-x}.}$

The continuous Bernoulli distribution arises in deep learning and computer vision, specifically in the context of variational autoencoders,^[4][5] for modeling the pixel intensities of natural images. As such, it defines a proper probabilistic counterpart for the commonly used binary cross entropy loss, which is often applied to continuous, ${\displaystyle [0,1]}$-valued data.^[6][7][8][9] This practice amounts to ignoring the normalizing constant of the continuous Bernoulli distribution, since the binary cross entropy loss only defines a true log-likelihood for discrete, ${\displaystyle \{0,1\}}$-valued data.

The continuous Bernoulli also defines an exponential family of distributions. Writing ${\displaystyle \eta =\log \left(\lambda /(1-\lambda )\right)}$ for the natural parameter, the density can be rewritten in canonical form: ${\displaystyle p(x|\eta )\propto \exp(\eta x)}$.

Related distributions

Bernoulli distribution

The continuous Bernoulli can be thought of as a continuous relaxation of the Bernoulli distribution, which is defined on the discrete set ${\displaystyle \{0,1\}}$ by the probability mass function:

${\displaystyle p(x)=p^{x}(1-p)^{1-x},}$

where ${\displaystyle p}$ is a scalar parameter between 0 and 1. Applying this same functional form on the continuous interval ${\displaystyle [0,1]}$ results in the continuous Bernoulli probability density function, up to a normalizing constant.

Beta distribution

The Beta distribution has the density function:

${\displaystyle p(x)\propto x^{\alpha -1}(1-x)^{\beta -1},}$

which can be re-written as:

${\displaystyle p(x)\propto x_{1}^{\alpha _{1}-1}x_{2}^{\alpha _{2}-1},}$

where ${\displaystyle \alpha _{1},\alpha _{2}}$ are positive scalar parameters, and ${\displaystyle (x_{1},x_{2})}$ represents an arbitrary point inside the 1-simplex, ${\displaystyle \Delta ^{1}=\{(x_{1},x_{2}):x_{1}>0,x_{2}>0,x_{1}+x_{2}=1\}}$. Switching the role of the parameter and the argument in this density function, we obtain:

${\displaystyle p(x)\propto \alpha _{1}^{x_{1}}\alpha _{2}^{x_{2}}.}$

This family is only identifiable up to the linear constraint ${\displaystyle \alpha _{1}+\alpha _{2}=1}$, whence we obtain:

${\displaystyle p(x)\propto \lambda ^{x_{1}}(1-\lambda )^{x_{2}},}$

corresponding exactly to the continuous Bernoulli density.

Exponential distribution

An exponential distribution restricted to the unit interval is equivalent to a continuous Bernoulli distribution with appropriate^[which?] parameter.

Continuous categorical distribution

The multivariate generalization of the continuous Bernoulli is called the continuous-categorical.^[10]

References