Rule of mixtures

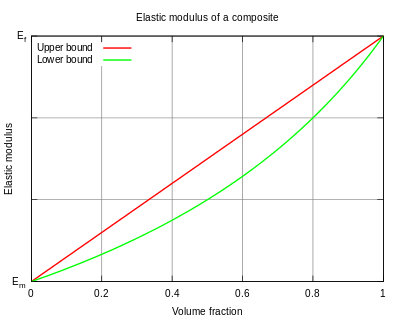
In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material .^[1][2][3] It provides a theoretical upper- and lower-bound on properties such as the elastic modulus, ultimate tensile strength, thermal conductivity, and electrical conductivity.^[3] In general there are two models, one for axial loading (Voigt model),^[2][4] and one for transverse loading (Reuss model).^[2][5]

In general, for some material property ${\displaystyle E}$ (often the elastic modulus^[1]), the rule of mixtures states that the overall property in the direction parallel to the fibers may be as high as

${\displaystyle E_{c}=fE_{f}+\left(1-f\right)E_{m}}$

where

• ${\displaystyle f={\frac {V_{f}}{V_{f}+V_{m}}}}$ is the volume fraction of the fibers
• ${\displaystyle E_{f}}$ is the material property of the fibers
• ${\displaystyle E_{m}}$ is the material property of the matrix

In the case of the elastic modulus, this is known as the upper-bound modulus, and corresponds to loading parallel to the fibers. The inverse rule of mixtures states that in the direction perpendicular to the fibers, the elastic modulus of a composite can be as low as

${\displaystyle E_{c}=\left({\frac {f}{E_{f}}}+{\frac {1-f}{E_{m}}}\right)^{-1}.}$

If the property under study is the elastic modulus, this quantity is called the lower-bound modulus, and corresponds to a transverse loading.^[2]

Derivation for elastic modulus

Voigt Modulus

Consider a composite material under uniaxial tension ${\displaystyle \sigma _{\infty }}$. If the material is to stay intact, the strain of the fibers, ${\displaystyle \epsilon _{f}}$ must equal the strain of the matrix, ${\displaystyle \epsilon _{m}}$. Hooke's law for uniaxial tension hence gives

${\displaystyle {\frac {\sigma _{f}}{E_{f}}}=\epsilon _{f}=\epsilon _{m}={\frac {\sigma _{m}}{E_{m}}}}$

(1)

where ${\displaystyle \sigma _{f}}$, ${\displaystyle E_{f}}$, ${\displaystyle \sigma _{m}}$, ${\displaystyle E_{m}}$ are the stress and elastic modulus of the fibers and the matrix, respectively. Noting stress to be a force per unit area, a force balance gives that

${\displaystyle \sigma _{\infty }=f\sigma _{f}+\left(1-f\right)\sigma _{m}}$

(2)

where ${\displaystyle f}$ is the volume fraction of the fibers in the composite (and ${\displaystyle 1-f}$ is the volume fraction of the matrix).

If it is assumed that the composite material behaves as a linear-elastic material, i.e., abiding Hooke's law ${\displaystyle \sigma _{\infty }=E_{c}\epsilon _{c}}$ for some elastic modulus of the composite ${\displaystyle E_{c}}$ and some strain of the composite ${\displaystyle \epsilon _{c}}$, then equations 1 and 2 can be combined to give

${\displaystyle E_{c}\epsilon _{c}=fE_{f}\epsilon _{f}+\left(1-f\right)E_{m}\epsilon _{m}.}$

Finally, since ${\displaystyle \epsilon _{c}=\epsilon _{f}=\epsilon _{m}}$, the overall elastic modulus of the composite can be expressed as^[6]

${\displaystyle E_{c}=fE_{f}+\left(1-f\right)E_{m}.}$

Reuss modulus

Now let the composite material be loaded perpendicular to the fibers, assuming that ${\displaystyle \sigma _{\infty }=\sigma _{f}=\sigma _{m}}$. The overall strain in the composite is distributed between the materials such that

${\displaystyle \epsilon _{c}=f\epsilon _{f}+\left(1-f\right)\epsilon _{m}.}$

The overall modulus in the material is then given by

${\displaystyle E_{c}={\frac {\sigma _{\infty }}{\epsilon _{c}}}={\frac {\sigma _{f}}{f\epsilon _{f}+\left(1-f\right)\epsilon _{m}}}=\left({\frac {f}{E_{f}}}+{\frac {1-f}{E_{m}}}\right)^{-1}}$

since ${\displaystyle \sigma _{f}=E\epsilon _{f}}$, ${\displaystyle \sigma _{m}=E\epsilon _{m}}$.^[6]

Other properties

Similar derivations give the rules of mixtures for

• mass density:
  $${\displaystyle \rho _{c}=\rho _{f}\centerdot f+\rho _{M}\centerdot (1-f)}$$

  
  where f is the atomic percent of fiber in the mixture.
• ultimate tensile strength:
  $${\displaystyle \left({\frac {f}{\sigma _{UTS,f}}}+{\frac {1-f}{\sigma _{UTS,m}}}\right)^{-1}\leq \sigma _{UTS,c}\leq f\sigma _{UTS,f}+\left(1-f\right)\sigma _{UTS,m}}$$

  
• thermal conductivity:
  $${\displaystyle \left({\frac {f}{k_{f}}}+{\frac {1-f}{k_{m}}}\right)^{-1}\leq k_{c}\leq fk_{f}+\left(1-f\right)k_{m}}$$

  
• electrical conductivity:
  $${\displaystyle \left({\frac {f}{\sigma _{f}}}+{\frac {1-f}{\sigma _{m}}}\right)^{-1}\leq \sigma _{c}\leq f\sigma _{f}+\left(1-f\right)\sigma _{m}}$$

  

See also

When considering the empirical correlation of some physical properties and the chemical composition of compounds, other relationships, rules, or laws, also closely resembles the rule of mixtures:

• Amagat's law – Law of partial volumes of gases
• Gladstone–Dale equation – Optical analysis of liquids, glasses and crystals
• Kopp's law – Uses mass fraction
• Kopp–Neumann law – Specific heat for alloys
• Richmann's law – Law for the mixing temperature
• Vegard's law – Crystal lattice parameters

References

External links

• Rule of mixtures calculator