Integral exponencial

En el ámbito de las matemáticas la integral exponencial es una función especial definida en el plano complejo e identificada con el símbolo  Ei.

Definiciones

Para valores reales de ${\displaystyle x}$, la integral exponencial ${\displaystyle Ei(x)}$ se define como

${\displaystyle {\mbox{Ei}}(x)=\int _{-\infty }^{x}{\frac {e^{t}}{t}}\,\mathrm {d} t.\,}$

Esta definición puede ser utilizada para valores positivos de ${\displaystyle x}$, pero a causa de la singularidad del integrando en cero, la integral debe ser interpretada en término del valor principal de Cauchy. Para valores complejos del argumento, esta definición es ambigua a causa de los puntos de ramificación en 0 y en ${\displaystyle \infty }$.^[1]​ En general, se realiza un corte en el eje real negativo y Ei puede ser definida mediante una continuación analítica en el resto del plano complejo.

Se utiliza la siguiente notación,^[2]​

${\displaystyle \mathrm {E} _{1}(z)=\int _{z}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t,\qquad |{\rm {Arg}}(z)|<\pi }$

Para valores positivos de la parte real de ${\displaystyle z}$, esto se puede expresar como^[3]​

${\displaystyle \mathrm {E} _{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,\mathrm {d} t,\qquad \Re (z)\geq 0.}$

El comportamiento de E₁ cerca del branch cut puede ser analizado mediante la siguiente relación:^[4]​

${\displaystyle \lim _{\delta \to 0\pm }\mathrm {E_{1}} (-x+i\delta )=-\mathrm {Ei} (x)\mp i\pi ,\qquad x>0,}$

Propiedades

Las propiedades de la exponencial integral mostradas, en ocasiones, permiten sortear él la evaluación explícita de la función a partir de la definición dada arriba.

Series Convergentes

Tras integrar la serie de Taylor de ${\displaystyle e^{-t}/t}$, y extraer la singularidad logarítmica, se puede obtener la siguiente representación en forma de serie de ${\displaystyle \mathrm {E_{1}} (x)}$ para ${\displaystyle x}$ real:^[5]​

${\displaystyle \mathrm {Ei} (x)=\gamma +\ln x+\sum _{k=1}^{\infty }{\frac {x^{k}}{k\;k!}}\qquad x>0}$

Para argumentos complejos fuera del eje real, esta serie se generaliza a^[6]​

${\displaystyle \mathrm {E_{1}} (z)=-\gamma -\ln z+\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}\qquad (|\mathrm {Arg} (z)|<\pi )}$

donde ${\displaystyle \gamma }$ es la constante de Euler-Mascheroni. La suma converge para todo ${\displaystyle z}$ complejo, y tomamos el valor usual del logaritmo complejo con el corte de rama a lo largo del eje real negativo.

Series Asintóticas

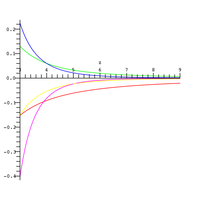
Por desgracia, la convergencia de las series mostradas arriba es muy lenta para argumentos con gran módulo. Por ejemplo, para ${\displaystyle x=10}$, se necesitan más de 40 términos para obtener una respuesta correcta con 3 cifras significativas.^[7]​ Sin embargo, existe una serie asintótica divergente que puede ser obtenida a partir de la integración de ${\displaystyle ze^{z}\mathrm {E_{1}} (z)}$ por partes:^[8]​

${\displaystyle \mathrm {E_{1}} (z)={\frac {\exp(-z)}{z}}\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}}$

cuyo error es del orden ${\displaystyle O(N!z^{-N})}$ y es válida para grandes valores de ${\displaystyle \mathrm {Re} (z)}$. El error relativo de la serie asintótica se muestra en la gráfica de la derecha para varios valores de ${\displaystyle N}$ (${\displaystyle N=1}$ en rojo, ${\displaystyle N=5}$ en rosa). Cuando ${\displaystyle x>40}$, la aproximación dada con ${\displaystyle N=40}$ es exacta en representación de doble precisión, de 64 bits.

Comportamiento exponencial y logarítmico: Cotas

De las series dadas arriba, se deduce que ${\displaystyle \mathrm {E_{1}} }$ se comporta como una exponencial negativa para grandes valores del argumento y como un logaritmo para pequeños valores del mismo. Para valores reales positivos del argumento, ${\displaystyle \mathrm {E_{1}} }$ queda acotada superior e inferiormente por funciones elementales como sigue:^[9]​

${\displaystyle {\frac {1}{2}}e^{-x}\,\ln \!\left(1+{\frac {2}{x}}\right)<\mathrm {E_{1}} (x)<e^{-x}\,\ln \!\left(1+{\frac {1}{x}}\right)\qquad x>0}$

La parte izquierda de la desigualdad se muestra en la gráfica de la izquierda en azul, la parte central, que es ${\displaystyle \mathrm {E_{1}} (x)}$, es la curva negra y la parte de la derecha es la curva roja.

Definición mediante ${\displaystyle \mathrm {Ein} }$

Las funciones ${\displaystyle \mathrm {Ei} }$ y ${\displaystyle \mathrm {E_{1}} }$ pueden ser escritas de forma más simple mediante la función entera ${\displaystyle \mathrm {Ein} }$^[10]​ definida como

${\displaystyle \mathrm {Ein} (z)=\int _{0}^{z}(1-e^{-t})\,{\frac {\mathrm {d} t}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}}$

(nótese que esta es la serie alternante que aparecía en la definición de ${\displaystyle \mathrm {E_{1}} }$). Se sigue inmediatamente que:

${\displaystyle \mathrm {E_{1}} (z)\,=\,-\gamma -\ln z+{\rm {Ein}}(z)\qquad |\mathrm {Arg} (z)|<\pi }$

${\displaystyle \mathrm {Ei} (x)\,=\,\gamma +\ln x-\mathrm {Ein} (-x)\qquad x>0}$

Relación con otras funciones

La integral exponencial está altamente relacionada con la función logaritmo integral ${\displaystyle li(x)}$ por la siguiente relación

${\displaystyle \mathrm {li} (x)=\mathrm {Ei} (\ln x)\,}$

para valores positivos reales de ${\displaystyle x}$.

La integral exponencial se puede generalizar a

${\displaystyle {\rm {E}}_{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,\mathrm {d} t,}$

que es una familia de funciones que puede representarse como un caso especial de la función gamma incompleta:^[11]​

${\displaystyle {\rm {E}}_{n}(x)=x^{n-1}\Gamma (1-n,x).\,}$

Esta forma generizada se llama a veces función de Misra function^[12]​ ${\displaystyle \varphi _{m}(x)}$, que se define como

${\displaystyle \varphi _{m}(x)={\rm {E}}_{-m}(x).\,}$

Derivadas

Las derivadas de las funciones ${\displaystyle \mathrm {E_{n}} }$ pueden ser obtenerse mediante el uso de la fórmula^[13]​

${\displaystyle \mathrm {E_{n}} '(z)=-\mathrm {E_{n-1}} (z)\qquad (n=1,2,3,\ldots )}$

Nótese que la función ${\displaystyle \mathrm {E_{0}} }$ es sencilla de evaluar (dando un término inicial a la relación recursiva), pues es ${\displaystyle e^{-z}/z}$.^[14]​

Integral Exponencial de argumento imaginario

Si ${\displaystyle z}$ es imaginario, la función tiene una parte real no nula, así podemos usar la fórmula

${\displaystyle \mathrm {E_{1}} (z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,\mathrm {d} t}$

para obtener una relación de la exponencial integral con las integrales trigonométricas ${\displaystyle \mathrm {Si} }$ y ${\displaystyle \mathrm {Ci} }$:

${\displaystyle \mathrm {E_{1}} (ix)=i\left(-{\frac {\pi }{2}}+\mathrm {Si} (x)\right)-\mathrm {Ci} (x)\qquad (x>0)}$

Las partes real e imaginaria de ${\displaystyle \mathrm {E_{1}} (x)}$ están dibujadas en la gráfica de la derecha en negro y rojo respectivamente.

Aplicaciones

• Transmisión de calor con dependencia temporal
• Flujo de aguas subterráneas fuera del equilibrio en la solución de Theis
• Transferencia radiativa en atmósferas estelares
• Ecuación de difusividad radial para flujos transitorios o de flujo no estacionario entre fuentes y sumideros con forma de línea recta.

Referencias

Véase también

• Logaritmo integral
• Seno integral
• Coseno integral
• Constante de Gompertz

Bibliografía

• Abramovitz, Milton; Irene Stegun (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Abramowitz and Stegun. New York: Dover. ISBN 0-486-61272-4. 
• Bender, Carl M.; Steven A. Orszag (1978). Advanced mathematical methods for scientists and engineers. McGraw-Hill. ISBN 0-07-004452-X.  La referencia utiliza el parámetro obsoleto |coautores= (ayuda)
• Bleistein, Norman; Richard A. Handelsman (1986). Asymptotic Expansions of Integrals. Dover. ISBN 0486650820.  La referencia utiliza el parámetro obsoleto |coautores= (ayuda)
• Misra, Rama Dhar (1940). «On the Stability of Crystal Lattices. II». Mathematical Proceedings of the Cambridge Philosophical Society 36 (2): 173. doi:10.1017/S030500410001714X. 
• Press, William H.; et al (1994). Numerical recipes in C: the art of scientific computing. Cambridge [England]: Cambridge University Press. ISBN 0-521-43108-5.  contiene códigos para calcular ${\displaystyle \mathrm {Ei} }$ y ${\displaystyle \mathrm {E_{1}} }$, a partir de p.222.

Enlaces externos

• Weisstein, Eric W. «Exponential Integral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Weisstein, Eric W. «En-Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Formulas and identities for Ei