Duopole de Cournot

Cet article est une ébauche concernant l’économie.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Le duopole de Cournot est un modèle économique utilisé pour décrire une structure industrielle dans laquelle les entreprises sont en concurrence par rapport à leurs volumes de production. Elles décident de ces volumes indépendamment les unes des autres, et ce à un même instant. Son nom vient d'Antoine-Augustin Cournot (1801-1877), un mathématicien qui le théorisa en observant le comportement d'entreprises au sein d'un duopole vendant de l'eau de source.

Cette théorie est conditionnée aux hypothèses suivantes :

• Il y a plus d'une entreprise et toutes les entreprises produisent un produit homogène, il n'y a donc pas de différenciation.
• Les firmes ne coopèrent pas, il n'y a pas de collusion.
• Les firmes ont un pouvoir de marché, elles sont donc faiseuses de prix (Price maker).
• Le nombre d'entreprises est fixe, il y a donc barrière à l'entrée.
• Les entreprises sont en concurrence sur les quantités, et non sur les prix, et choisissent leurs quantités simultanément.
• Les entreprises sont rationnelles, et recherchent la maximisation du profit.

Dès que l'on relâche l'hypothèse de la simultanéité de la fixation des quantités, nous sommes face à un duopole à la Stackelberg, c'est-à-dire que les firmes fixent successivement les quantités offertes. La première sera leader en quantité et la seconde suiveuse.

Présentation du modèle

La méthode d'analyse du duopole revient à trouver l'équilibre de Nash du jeu dans lequel deux firmes choisissent simultanément leur niveau de production.

Ce jeu est défini comme suit :

• Joueurs : les deux firmes (${\displaystyle 1}$ et ${\displaystyle 2}$)
• Actions : chaque firme choisit la quantité qu'elle produit (${\displaystyle q_{1}}$ et ${\displaystyle q_{2}}$)
• Paiements : profits de la firme ${\displaystyle i\in \{1,2\}}$${\displaystyle \pi _{i}(q_{1},q_{2})=P(q_{1}+q_{2})q_{i}-C_{i}(q_{i})}$

Résolution dans le cas linéaire

• La fonction de demande est linéaire : ${\displaystyle P(Q)=a-bQ}$, où ${\displaystyle Q=q_{1}+q_{2}}$ est la quantité totale produite sur le marché.
• La fonction de coût est linéaire : ${\displaystyle C_{i}(q_{i})=c_{i}q_{i}}$, où ${\displaystyle (a,b,c_{1},c_{2})\in \mathbb {R} _{+}^{4}}$ sont tous positifs, et ${\displaystyle c_{i}<a}$ pour ${\displaystyle i=1,2}$.

${\displaystyle (q_{1}^{c},q_{2}^{c})}$ est un équilibre de Cournot (ou Cournot-Nash) si :

${\displaystyle {\begin{cases}q_{1}^{c}&{\text{est solution de }}{\underset {q_{1}}{\max }}\pi _{1}(q_{1},q_{2}^{c})\\q_{2}^{c}&{\text{est solution de }}{\underset {q_{1}}{\max }}\pi _{2}(q_{1}^{c},q_{2})\end{cases}}}$

C'est bien un équilibre de Nash du jeu défini plus haut puisque chaque joueur joue sa meilleure réponse à la stratégie d'équilibre de l'autre joueur.

Pour obtenir l'équilibre, il faut analyser les fonctions de meilleure réponse de chacune des deux firmes. Pour une quantité ${\displaystyle q_{2}}$ produite par la firme ${\displaystyle 2}$, le profit de la firme ${\displaystyle 1}$ est${\displaystyle \pi _{1}(q_{1},q_{2})=(a-b(q_{1}+q_{2}))q_{1}-c_{1}q_{1}}$

L'entreprise ${\displaystyle 1}$ choisit la quantité ${\displaystyle q_{1}}$ de manière à maximiser ${\displaystyle \pi _{1}(q_{1},q_{2})}$ (l'entreprise ${\displaystyle 1}$ ne peut bien sûr pas avoir d'impact sur ${\displaystyle q_{2}}$, elle considère donc ${\displaystyle q_{2}}$ comme une donnée de son problème). Cette quantité est maximisée lorsque sa derivée s'annule:${\displaystyle {\frac {\partial \pi _{1}(q_{1},q_{2})}{\partial q_{1}}}=a-bq_{2}-2bq_{1}-c_{1}=0}$

Ce qui donne :${\displaystyle q_{1}=R_{1}(q_{2})={\frac {a-c_{1}}{2b}}-{\frac {1}{2}}q_{2}}$

${\displaystyle q_{2}\mapsto R_{1}(q_{2})}$ est appelée la fonction de meilleure réponse (ou fonction de réaction) de la firme ${\displaystyle 1}$. Pour toute quantité ${\displaystyle q_{2}}$ produite par le concurrent, ${\displaystyle R_{1}(q_{2})}$ indique la quantité qui maximise le profit de l'entreprise ${\displaystyle 1}$.

Par symétrie, la fonction de meilleure réponse de la firme ${\displaystyle 2}$ est :${\displaystyle q_{2}=R_{2}(q_{1})={\frac {a-c_{2}}{2b}}-{\frac {1}{2}}q_{1}}$

Les fonctions de meilleure réponse sont décroissantes. On dit que les quantités sont des substituts stratégiques : plus une firme produit, moins sa concurrence à intérêt à produire.

Intuitivement, si une firme produit davantage, le prix auquel la firme concurrente peut vendre décroît toutes choses égales par ailleurs, la marge est donc réduite, et l'incitation à produire moindre.

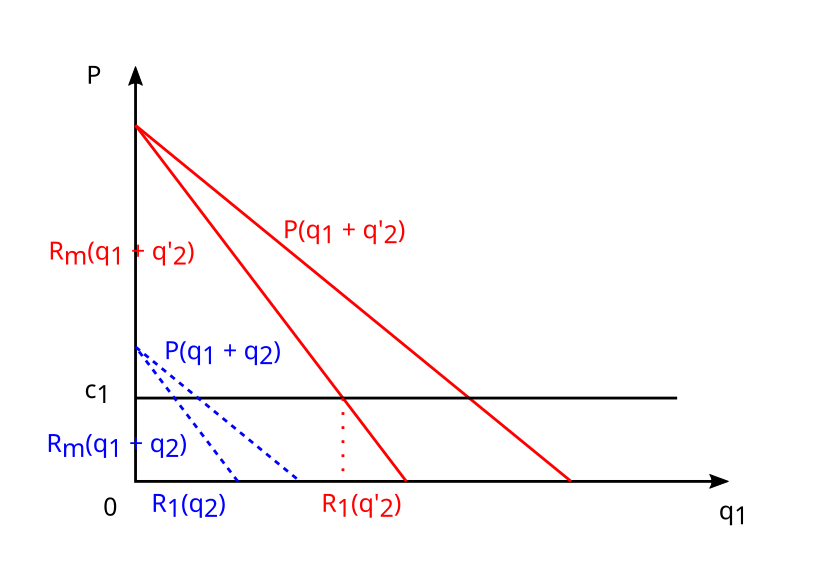
Le graphique ci-dessus, dans lequel est représentée la demande résiduelle de l'entreprise ${\displaystyle 1}$ pour deux valeurs différentes de ${\displaystyle q_{2}}$, illustre ce concept. La demande résiduelle mesure la demande individuellement reçue par une firme donnée étant donné un niveau de production de l'autre firme. Ainsi, la demande (inverse) est une fonction de ${\displaystyle q_{1}+q_{2}}$, tandis que la demande résiduelle de la firme ${\displaystyle 1}$ est une fonction de ${\displaystyle q_{1}}$ pour un niveau de production ${\displaystyle q_{2}}$ donné. Ainsi, dans le cas où la demande est linéaire, la demande résiduelle est toujours une droite parallèle à la courbe de demande inverse, et plus ${\displaystyle q_{2}}$ s'accroît, plus la droite de demande résiduelle de la firme ${\displaystyle 1}$ se déplace vers la gauche. Par exemple, lorsque l'entreprise ${\displaystyle 2}$ augmente sa production de ${\displaystyle q'_{2}}$ (droite pleine) à ${\displaystyle q_{2}}$ (droite en pointillés), avec ${\displaystyle q_{2}>q'2}$, le prix de marché en fonction de ${\displaystyle q_{1}}$ baisse de ${\displaystyle P(q1+q'_{2})}$ à ${\displaystyle P(q_{1}+q_{2})}$. Le nouveau revenu marginal est donc lui aussi translaté vers l'intérieur du graphe. Comme le coût reste inchangé, la solution du problème de maximisation donnée par ${\displaystyle R_{m}=C_{m}}$ est donc décalée vers la gauche. Ainsi ${\displaystyle R_{1}(q_{2})<R_{1}(q'_{2})}$.

Parce que la fonction de demande est linéaire, sa pente ne dépend pas des quantités produites.

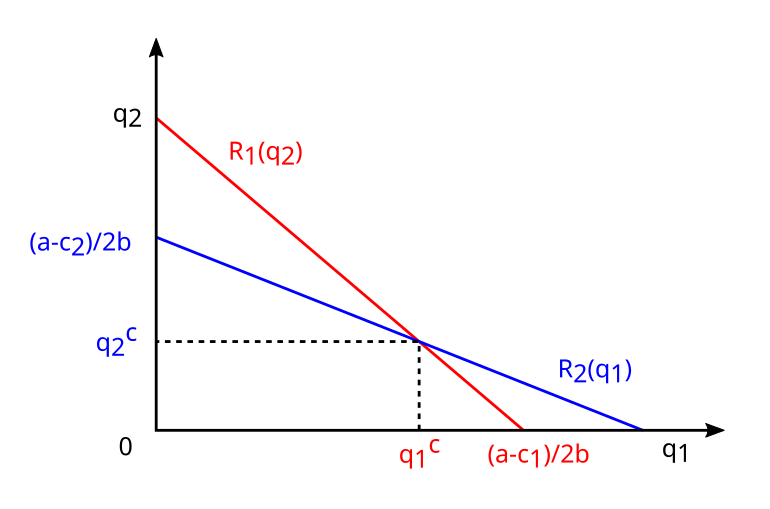
Il faut alors résoudre le système suivant :

${\displaystyle {\begin{cases}q_{1}^{c}=R_{1}(q_{2}^{c})&(1)\\q_{2}^{c}=R_{2}(q_{1}^{c})&(2)\end{cases}}}$

En remplaçant ${\displaystyle q_{2}^{c}=R_{2}(q_{1}^{c})={\frac {a-c2}{2b}}-{\frac {1}{2}}q_{1}^{c}}$ dans ${\displaystyle (1)}$, on obtient :

${\displaystyle {\begin{aligned}q_{1}^{c}&={\frac {a-c_{1}}{2b}}-{\frac {1}{2}}\left({\frac {a-c_{2}}{2b}}-{\frac {1}{2}}q_{1}^{c}\right)\\\iff {\frac {3}{4}}q_{1}^{c}&={\frac {2a-2c_{1}-a+c_{2}}{4b}}\\\iff q_{1}^{c}&={\frac {a-2c_{1}+c_{2}}{3b}}\end{aligned}}}$

On en déduit :

${\displaystyle {\begin{aligned}q_{2}^{c}&=R_{2}(q_{1}^{c})={\frac {a-c_{2}}{2b}}-{\frac {1}{2}}\left({\frac {a-2c_{1}+c_{2}}{3b}}\right)\\\iff q_{2}^{c}&={\frac {3a-3c_{2}-a+2c_{1}-c_{2}}{6b}}\\\iff q_{2}^{c}&={\frac {a-2c_{2}+c_{1}}{3b}}\end{aligned}}}$

La quantité totale offerte sur le marché est :${\displaystyle Q^{c}=q_{1}^{c}+q_{2}^{c}={\frac {2a-c_{1}-c_{2}}{3b}}}$

Le prix correspondant est :${\displaystyle p^{c}=a-bQ^{c}={\frac {a+c_{1}+c_{2}}{3}}}$

Enfin, les profits se calculent ainsi :${\displaystyle \pi _{1}^{c}=(p^{c}-c_{1})q_{1}^{c}={\frac {a-2c_{1}+c_{2}}{3}}\times {\frac {a-2c_{1}+c_{2}}{3b}}={\frac {(a-2c_{1}+c_{2})^{2}}{9b}}}$

De même,${\displaystyle \pi _{2}^{c}=(p^{c}-c_{2})q_{2}^{c}={\frac {a-2c_{2}+c_{1}}{3}}\times {\frac {a-2c_{2}+c_{1}}{3b}}={\frac {(a-2c_{2}+c_{1})^{2}}{9b}}}$

On remarque que ${\displaystyle \pi _{i}^{c}=b(q_{i}^{c})^{2}}$, ${\displaystyle i\in \{1,2\}}$.

Si les firmes sont symétriques, alors ${\displaystyle c_{1}=c_{2}=c}$, et :

${\displaystyle q_{1}^{c}=q_{2}^{c}=q^{c}={\frac {a-c}{3b}};~Q^{c}=2q^{c}={\frac {2(a-c)}{3b}}}$

${\displaystyle p^{c}={\frac {a+2c}{3}}}$

${\displaystyle \pi _{1}=\pi _{2}={\frac {(a-c)^{2}}{9b}}}$

Extension du modèle à ${\displaystyle n}$ firmes : Oligopole de Cournot

Cas de ${\displaystyle n}$ firmes identiques

Résolution dans le cas linéaire

Soit ${\displaystyle n}$ firmes identiques (toutes ont le même coût marginal ${\displaystyle c}$). Soit ${\displaystyle q_{\overline {i}}}$ la quantité produite par toutes les autres firmes que la firme ${\displaystyle i}$. Le problème de la firme ${\displaystyle i}$ peut s'écrire :${\displaystyle {\underset {q_{i}}{\max }}\pi _{i}\left((q_{k})_{k\in [\![1,n]\!]}\right)=(a-b(q_{i}+q_{\overline {i}})-c)q_{i}}$

Ce qui donne${\displaystyle R_{i}(q_{\overline {i}})={\frac {a-c}{2b}}-{\frac {1}{2}}q_{\overline {i}}(3)}$

On remarque que la fonction de meilleure réponse d’une firme ne dépend pas des quantités individuelles des autres firmes, mais de la quantité totale produite par les concurrents ${\displaystyle q_{\overline {i}}}$.

Un équilibre de Nash est donc un ensemble de quantités ${\displaystyle ((q_{k}^{c})_{k\in [\![1,n]\!]})}$ tel que :${\displaystyle \forall k\in [\![1,n]\!],~q_{k}^{c}={\frac {a-c}{2b}}-{\frac {1}{2}}\sum _{1\leq j\leq n,~j\neq k}q_{j}^{c}}$

Puisque toutes les firmes sont symétriques, elles doivent toutes produire la même quantité. Ainsi ${\displaystyle \forall k\in [\![1,n]\!],~q_{k}^{c}=q^{c}}$. En remplaçant tous les ${\displaystyle q_{i}^{c}}$ par ${\displaystyle q^{c}}$, on obtient :${\displaystyle q^{c}={\frac {a-c}{2b}}-{\frac {n-1}{2}}q^{c}}$

Ainsi, ${\displaystyle q^{c}={\frac {a-c}{b(n+1)}}}$

Donc${\displaystyle Q^{c}=nq^{c}={\frac {n}{n+1}}{\frac {a-c}{b}}}$,

et ${\displaystyle p^{c}=a-bQ^{c}={\frac {a+nc}{n+1}}}$.

Enfin, pour toutes les firmes ${\displaystyle i}$${\displaystyle \pi _{i}=\pi =(p^{c}-c)q^{c}={\frac {1}{b}}\left({\frac {a-c}{n+1}}\right)^{2}}$

Comparaison avec concurrence parfaite et monopole

En concurrence pure et parfaite, on doit avoir ${\displaystyle p=C_{m}=c}$. Le seul prix d'équilibre possible est donc ${\displaystyle p^{*}=c}$, ce qui donne une quantité totale produite de ${\displaystyle Q^{*}={\frac {a-c}{b}}}$.

En monopole, ${\displaystyle Q^{M}}$ maximise ${\displaystyle (a-bq-c)q}$, ce qui donne ${\displaystyle Q^{M}={\frac {a-c}{2b}}}$, et ${\displaystyle p^{M}={\frac {a+c}{2}}}$

Ainsi, ${\displaystyle Q^{M}<Q^{c}<Q^{*}}$ et ${\displaystyle p^{*}<p^{c}<p^{M}}$.

C’est en concurrence parfaite que la production totale est la plus grande (et donc le prix le plus faible), et en monopole que la production est la moindre (et donc le prix le plus élevé). L’oligopole de Cournot est une situation intermédiaire.

Par ailleurs, plus ${\displaystyle n}$ est grand, plus la quantité est élevée et le prix faible. Quand ${\displaystyle n\to \infty }$, on remarque que ${\displaystyle Q_{c}\to Q^{*}}$ et ${\displaystyle p^{c}\to c=p^{*}}$. Quand ${\displaystyle n=1}$, on retrouve ${\displaystyle Q^{c}=Q^{M}}$ et ${\displaystyle p^{c}=p^{M}}$.

• Portail de l’économie