Intersection (géométrie)

Pour les articles homonymes, voir Intersection.

En géométrie, une intersection est un point, une ligne ou une courbe commune à deux objets ou plus (tels que des droites, des courbes, des plans et des surfaces). Le cas le plus simple en géométrie euclidienne est l'intersection entre deux droites distinctes, qui est soit un point, soit inexistante (si les lignes sont parallèles). Les autres types d'intersection géométrique comprennent :

• Intersection d'une droite et d'un plan (en)
• Intersection d'une droite et d'une sphère (en)
• Intersection d'une droite et d'un polyèdre (en)
• Intersection d'une droite et d'un segment (en)
• Courbe d'intersection

La détermination de l'intersection d'hyperplans – des objets géométriques linéaires dans un espace de dimension supérieure – est une tâche simple d'algèbre linéaire, qui revient à déterminer la solution d'un système d'équations linéaires. En général, la détermination d'une intersection conduit à des équations non linéaires, qui peuvent être résolues numériquement, par exemple en utilisant la méthode de Newton. Les problèmes d'intersection entre une droite et une conique (cercle, ellipse, parabole, etc.) ou une quadrique (sphère, cylindre, hyperboloïde, etc.) conduisent à des équations du second degré simples à résoudre. Les intersections entre quadriques conduisent à des équations quartiques qui peuvent être résolues algébriquement.

Dans un plan

Deux droites

Pour la détermination du point d'intersection de deux lignes non parallèles

${\displaystyle a_{1}x+b_{1}y=c_{1},\ a_{2}x+b_{2}y=c_{2}}$

on obtient, à partir de la règle de Cramer ou en substituant une variable, les coordonnées du point d'intersection ${\displaystyle (x_{s},y_{s})}$ :

${\displaystyle x_{s}={\frac {c_{1}b_{2}-c_{2}b_{1}}{a_{1}b_{2}-a_{2}b_{1}}},\quad y_{s}={\frac {a_{1}c_{2}-a_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}}.\ }$

(Si ${\displaystyle a_{1}b_{2}-a_{2}b_{1}=0}$ alors les lignes sont parallèles, donc l'intersection n'existe pas, et ces formules ne peuvent pas être utilisées car elles impliquent une division par 0).

Deux segments de droite

Pour deux segments de ligne non parallèles ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$ et ${\displaystyle (x_{3},y_{3}),(x_{4},y_{4})}$ il n'y a pas nécessairement de point d'intersection (voir schéma), car le point d'intersection ${\displaystyle (x_{0},y_{0})}$ des droites correspondantes n'ont pas besoin d'être contenues dans les segments de droite. Afin de vérifier la situation, on utilise des représentations paramétriques des droites :

${\displaystyle (x(s),y(s))=(x_{1}+s(x_{2}-x_{1}),y_{1}+s(y_{2}-y_{1})),}$

${\displaystyle (x(t),y(t))=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3})).}$

Les segments de droite ne se croisent qu'en un point commun ${\displaystyle (x_{0},y_{0})}$ des lignes correspondantes si les paramètres correspondants ${\displaystyle s_{0},t_{0}}$ remplissent la condition ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$ . Les paramètres ${\displaystyle s_{0},t_{0}}$ sont la solution du système linéaire

${\displaystyle s(x_{2}-x_{1})-t(x_{4}-x_{3})=x_{3}-x_{1},}$

${\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3})=y_{3}-y_{1}\ .}$

Il peut être résolu pour s et t en utilisant la règle de Cramer (voir supra). Si la condition ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$ est remplie on insère ${\displaystyle s_{0}}$ ou ${\displaystyle t_{0}}$ dans la représentation paramétrique correspondante et on obtient le point d'intersection ${\displaystyle (x_{0},y_{0})}$ .

Exemple : Pour les segments de droite d'extrémités ${\displaystyle (1,1),(3,2)}$ et ${\displaystyle (1,4),(2,-1)}$, on obtient le système linéaire

${\displaystyle 2s-t=0}$

${\displaystyle s+5t=3}$

et ${\displaystyle s_{0}={\tfrac {3}{11}},t_{0}={\tfrac {6}{11}}}$ . Ainsi, les droites se coupent au point ${\displaystyle ({\tfrac {17}{11}},{\tfrac {14}{11}})}$ .

Remarque : En considérant des droites, au lieu de segments, déterminés par des paires de points, chaque condition ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$ peut être supprimée et la méthode donne le point d'intersection des droites.

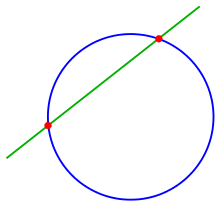
Une droite et un cercle

Pour l'intersection de la droite d'équation ${\displaystyle ax+by=c}$ et le cercle ${\displaystyle x^{2}+y^{2}=r^{2}}$, on résout l'équation de droite pour x ou y et on la substitue dans l'équation du cercle et on obtient la solution (en utilisant la formule d'une équation du second degré) ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$ avec

${\displaystyle x_{1/2}={\frac {ac\pm b{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{a^{2}+b^{2}}}\ ,}$

${\displaystyle y_{1/2}={\frac {bc\mp a{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{a^{2}+b^{2}}}\,}$

si ${\displaystyle r^{2}(a^{2}+b^{2})-c^{2}>0\ .}$

On a alors trois cas :

• si cette condition est vérifiée avec une inégalité stricte, il y a deux points d'intersection ; dans ce cas, la droite est appelée une droite sécante du cercle et le segment de droite reliant les points d'intersection est appelé une corde du cercle.
• si on est dans le cas d'égalité ${\displaystyle r^{2}(a^{2}+b^{2})-c^{2}=0}$ , il n'existe qu'un seul point d'intersection et la droite est tangente au cercle
• si l'inégalité n'est pas vérifié, la droite ne coupe pas le cercle.

Si le centre du cercle n'est pas à l'origine, on peut s'y ramener^[1].

L'intersection d'une droite et d'une parabole ou d'une hyperbole peut être traitée de manière analogue.

Deux cercles

La détermination des points d'intersection de deux cercles

${\displaystyle (x-x_{1})^{2}+(y-y_{1})^{2}=r_{1}^{2},\ \quad (x-x_{2})^{2}+(y-y_{2})^{2}=r_{2}^{2}}$

se ramène au cas précédent de l'intersection d'une droite et d'un cercle. Par différence des deux équations données on obtient l'équation de droite :

${\displaystyle 2(x_{2}-x_{1})x+2(y_{2}-y_{1})y=r_{1}^{2}-x_{1}^{2}-y_{1}^{2}-r_{2}^{2}+x_{2}^{2}+y_{2}^{2}.}$

Cette droite spéciale est l'axe radical des deux cercles.

Cas particulier ${\displaystyle \;x_{1}=y_{1}=y_{2}=0}$ : Dans ce cas, l'origine est le centre du premier cercle et le deuxième centre se trouve sur l'axe des abscisses (voir schéma). L'équation de la droite radicale se simplifie en ${\displaystyle \;2x_{2}x=r_{1}^{2}-r_{2}^{2}+x_{2}^{2}\;}$ et les points d'intersection peuvent s'écrire ${\displaystyle (x_{0},\pm y_{0})}$ avec

${\displaystyle x_{0}={\frac {r_{1}^{2}-r_{2}^{2}+x_{2}^{2}}{2x_{2}}},\quad y_{0}={\sqrt {r_{1}^{2}-x_{0}^{2}}}\ .}$

Dans le cas où ${\displaystyle r_{1}^{2}<x_{0}^{2}}$ les cercles n'ont aucun point commun.

Si ${\displaystyle r_{1}^{2}=x_{0}^{2}}$ les cercles ont un point commun et l'axe radical est la tangente commune.

Tout cas général tel qu'écrit ci-dessus peut être ramené par une translation et une rotation au cas particulier.

L'intersection de deux disques (l'intérieur des deux cercles) forme une forme appelée lentille.

Deux sections coniques

Le problème de l'intersection d'une ellipse/hyperbole/parabole avec une autre section conique conduit à un système d'équations quadratiques, qui peut être résolu facilement dans des cas particuliers par élimination d'une coordonnée. Les propriétés spéciales des sections coniques peuvent être utilisées pour obtenir une solution. En général, les points d'intersection peuvent être déterminés en résolvant l'équation par une méthode de Newton. Si a) les deux coniques sont données implicitement (par une équation) une méthode de Newton bidimensionnelle b) l'une implicitement et l'autre paramétriquement donnée une méthode de Newton unidimensionnelle est nécessaire, comme détaillé par la suite.

Deux courbes lisses

Deux courbes dans ${\displaystyle \mathbb {R} ^{2}}$ (espace à deux dimensions), qui sont continûment différentiables (c'est-à-dire qu'il n'y a pas de courbure prononcée), ont un point d'intersection, s'ils ont un point du plan en commun et ont en ce point

• deux tangentes différentes ( intersection transversale ), ou
• une tangente en commun qui se croisent ( intersection touchante, voir schéma).

Si les deux courbes ont un point S et la droite tangente en commun mais ne se croisent pas, elles se touchent juste au point S .

Étant donné que les intersections touchantes apparaissent rarement et sont difficiles à gérer, les considérations suivantes omettent ce cas. Dans tous les cas ci-dessous, toutes les conditions nécessaires sur les dérivées sont présupposées. La détermination des points d'intersection conduit toujours à une ou deux équations non linéaires qui peuvent être résolues par itération de Newton. Une liste des cas apparaissant suit :

• si les deux courbes sont explicitement données : ${\displaystyle y=f_{1}(x),\ y=f_{2}(x)}$, leur mise en équation donne l'équation

${\displaystyle f_{1}(x)=f_{2}(x)\ .}$

• si les deux courbes sont données par leurs équations paramétriques : ${\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:(x_{2}(s),y_{2}(s)).}$

Leur mise en équation donne deux équations à deux variables :

${\displaystyle x_{1}(t)=x_{2}(s),\ y_{1}(t)=y_{2}(s)\ .}$

• si une courbe est déterminée paramétriquement et l'autre implicitement donnée : ${\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:f(x,y)=0.}$

C'est le cas le plus simple en dehors du cas explicite. Il faut substituer la représentation paramétrique de ${\displaystyle C_{1}}$ dans l'équation ${\displaystyle f(x,y)=0}$ de courbe ${\displaystyle C_{2}}$ et on obtient l'équation :

${\displaystyle f(x_{1}(t),y_{2}(t))=0\ .}$

• si les deux courbes sont implicitement données : ${\displaystyle C_{1}:f_{1}(x,y)=0,\ C_{2}:f_{2}(x,y)=0.}$

Ici, un point d'intersection est une solution du système

${\displaystyle f_{1}(x,y)=0,\ f_{2}(x,y)=0\ .}$

Toute itération de Newton nécessite des valeurs de départ pratiques, qui peuvent être estimées par une visualisation des deux courbes. Une courbe paramétrique ou explicite peut être facilement visualisée, car à tout paramètre t ou x respectivement il est facile de calculer le point correspondant. Pour les courbes implicites, cette tâche n'est pas aussi facile. Dans ce cas, il faut déterminer un point de courbe à l'aide de valeurs de départ et d'une itération ^[2]

Exemples:

1. une courbe paramétrique ${\displaystyle C_{1}:(t,t^{3})}$ et un cercle ${\displaystyle C_{2}:(x-1)^{2}+(y-1)^{2}-10=0}$ (voir schéma).

La méthode de Newton ${\displaystyle t_{n+1}:=t_{n}-{\frac {f(t_{n})}{f'(t_{n})}}}$ pour la fonction

${\displaystyle f(t)=(t-1)^{2}+(t^{3}-1)^{2}-10}$ doit être fait. Comme valeurs de départ, on peut choisir −1 et 1,5.

Les points d'intersection sont : (−1,1073 ; −1,3578), (1,6011 ; 4,1046)

1. ${\displaystyle C_{1}:f_{1}(x,y)=x^{4}+y^{4}-1=0,}$

${\displaystyle C_{2}:f_{2}(x,y)=(x-0.5)^{2}+(y-0.5)^{2}-1=0}$ (voir schéma).

La méthode de Newton

${\displaystyle {x_{n+1} \choose y_{n+1}}={x_{n}+\delta _{x} \choose y_{n}+\delta _{y}}}$ doit être effectuée, où ${\displaystyle {\delta _{x} \choose \delta _{y}}}$ est la solution du système linéaire

${\displaystyle {\begin{pmatrix}{\frac {\partial f_{1}}{\partial x}}&{\frac {\partial f_{1}}{\partial y}}\\{\frac {\partial f_{2}}{\partial x}}&{\frac {\partial f_{2}}{\partial y}}\end{pmatrix}}{\delta _{x} \choose \delta _{y}}={-f_{1} \choose -f_{2}}}$ au point ${\displaystyle (x_{n},y_{n})}$ . Comme valeurs de départ on peut choisir (−0,5 ;1) et (1 ; −0,5).

Le système linéaire peut être résolu par la règle de Cramer.

Les points d'intersection sont (−0,3686 ; 0,9953) et (0,9953 ; −0,3686).

Deux polygones

Si l'on veut déterminer les points d'intersection de deux polygones, on peut vérifier l'intersection de n'importe quelle paire de segments de droite des polygones (voir le cas de deux droites concourantes). Pour les polygones avec de nombreux segments, cette méthode est plutôt chronophage. En pratique on accélère l'algorithme d'intersection en utilisant des tests de fenêtre . Dans ce cas, on divise les polygones en petits sous-polygones et on détermine la plus petite fenêtre (rectangle avec des côtés parallèles aux axes de coordonnées) pour tout sous-polygone. Avant de commencer la détermination fastidieuse du point d'intersection de deux segments de ligne, toute paire de fenêtres est testée pour les points communs^[3].

En trois dimensions

Dans l'espace tridimensionnel, il existe des points d'intersection (points communs) entre les courbes et les surfaces. Dans les sections suivantes, seule l'intersection transversale est considérée.

Une droite et un plan

L'intersection d'une droite et d'un plan en position générale en trois dimensions est un point.

Généralement, une droite dans l'espace a une représentation paramétrique de la forme ${\displaystyle (x(t),y(t),z(t))}$ et un plan par une équation ${\displaystyle ax+by+cz=d}$ . L'insertion de la représentation des paramètres dans l'équation donne l'équation linéaire

${\displaystyle ax(t)+by(t)+cz(t)=d\ ,}$

pour paramètre ${\displaystyle t_{0}}$ du point d'intersection ${\displaystyle (x(t_{0}),y(t_{0}),z(t_{0}))}$ .

Si l'équation linéaire n'a pas de solution, la droite se trouve sur le plan ou lui est parallèle.

Trois plans

Si une droite est définie par deux plans sécants ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2}$ et doit être intersectée par un troisième plan ${\displaystyle \varepsilon _{3}:\ {\vec {n}}_{3}\cdot {\vec {x}}=d_{3}}$, le point d'intersection commun des trois plans doit être évalué.

Trois avions ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2,3}$ avec des vecteurs normaux indépendants linéaires ${\displaystyle {\vec {n}}_{1},{\vec {n}}_{2},{\vec {n}}_{3}}$ ont pour point d'intersection

${\displaystyle {\vec {p}}_{0}={\frac {d_{1}({\vec {n}}_{2}\times {\vec {n}}_{3})+d_{2}({\vec {n}}_{3}\times {\vec {n}}_{1})+d_{3}({\vec {n}}_{1}\times {\vec {n}}_{2})}{{\vec {n}}_{1}\cdot ({\vec {n}}_{2}\times {\vec {n}}_{3})}}\ .}$

Pour le prouver, il faut établir ${\displaystyle {\vec {n}}_{i}\cdot {\vec {p}}_{0}=d_{i},\ i=1,2,3,}$ en utilisant les règles du produit mixte. Si celui-ci est nul, alors on est dans un cas dégénéré et il n'y a pas d'intersection, ou c'est une droite (ou un plan, si les trois plans sont identiques).

Une courbe et une surface

De manière analogue au cas plan, les cas suivants conduisent à des systèmes non linéaires, qui peuvent être résolus à l'aide d'une itération de Newton à 1 ou 3 dimensions^[4].

• courbe paramétrique ${\displaystyle C:(x(t),y(t),z(t))}$ et surface paramétrique ${\displaystyle S:(x(u,v),y(u,v),z(u,v))\ ,}$

• courbe paramétrique ${\displaystyle C:(x(t),y(t),z(t))}$ et surface implicite ${\displaystyle S:f(x,y,z)=0\ .}$

Exemple

• la courbe paramétrique ${\displaystyle C:(t,t^{2},t^{3})}$ et la surface implicite ${\displaystyle S:x^{4}+y^{4}+z^{4}-1=0}$ (voir image) ;
• les points d'intersection sont : (−0,8587 ; 0,7374 ; −0,6332), (0,8587 ; 0,7374 ; 0,6332).

Une intersection droite-sphère est un cas particulier simple.

Comme dans le cas d'une droite et d'un plan, l'intersection d'une courbe et d'une surface en position générale est constituée de points discrets, mais une courbe peut être partiellement ou totalement contenue dans une surface.

Une droite et un polyèdre

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Deux surfaces

Deux surfaces sécantes transversalement donnent une courbe d'intersection. Le cas le plus simple est la droite d'intersection de deux plans non parallèles.

Voir aussi

• Géométrie analytique#Intersections
• Géométrie algorithmique
• Équation de droite
• Intersection (mathématiques)

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Intersection (geometry) » (voir la liste des auteurs).

Bibliographie

• Nicholas M. Patrikalakis et Takashi Maekawa, Interrogation de forme pour la conception et la fabrication assistées par ordinateur, Springer, 2002, , 9783540424543, p. 408. [1]

• Portail de la géométrie