Théorème de Girsanov

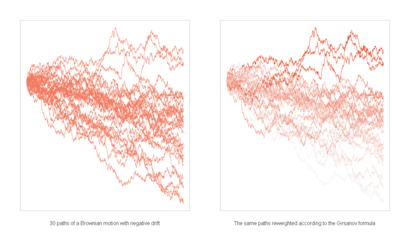
Dans la théorie des probabilités, le théorème de Girsanov indique comment un processus stochastique change si l'on change de mesure. Ce théorème est particulièrement important dans la théorie des mathématiques financières dans le sens où il donne la manière de passer de la probabilité historique qui décrit la probabilité qu'un actif sous-jacent (comme le prix d'une action ou un taux d'intérêt) prenne dans le futur une valeur donnée à la probabilité risque neutre qui est un outil très utile pour évaluer la valeur d'un dérivé du sous-jacent.

Historique

Des résultats de ce type ont été prouvés pour la première fois dans les années 1940 par Cameron-Martin puis en 1960 par Girsanov. Par la suite ils ont été étendus à des classes plus vastes de processus allant en 1977 jusqu'à la forme générale de Lenglart.

Énoncé du théorème

Soit ${\displaystyle X_{t}}$ une martingale locale continue par rapport à une filtration ${\displaystyle ({\mathcal {F}}_{t})_{t\geq 0}}$ satisfaisant les conditions usuelles. On définit l'exponentielle stochastique ${\displaystyle Z}$ de ${\displaystyle X}$ par la formule

${\displaystyle Z_{t}=\exp \left(X_{t}-{\frac {1}{2}}\langle X\rangle _{t}\right),}$

avec ${\displaystyle \langle X\rangle _{t}}$ la Variation quadratique de ${\displaystyle X_{t}}$. Notamment, on a l'équation différentielle stochastique : ${\displaystyle dZ_{t}=Z_{t}dX_{t}.}$

Le processus ${\displaystyle Z}$ est alors une martingale locale strictement positive, et on peut définir une mesure ${\displaystyle Q_{t}}$ équivalente à la restriction de la mesure P à ${\displaystyle {\mathcal {F}}_{t}}$ à partir de sa densité de Radon-Nikodym.

${\displaystyle {\frac {dQ_{t}}{dP_{|_{{\mathcal {F}}_{t}}}}}=Z_{t}.}$

Si ${\displaystyle Z}$ est en fait une vraie martingale, la famille ${\displaystyle Q_{t}}$ est induite par une mesure Q définie sur toute la tribu ${\displaystyle {\mathcal {F}}}$ :

${\displaystyle Q_{t}=Q_{|_{{\mathcal {F}}_{t}}}.}$

De plus, si Y est une martingale locale sous P alors le processus

${\displaystyle {\widetilde {Y}}_{t}=Y_{t}-\left[Y,X\right]_{t}}$

est une martingale locale sous Q.

Corollaire

Si X est un processus continu et W est un mouvement brownien sous P alors

${\displaystyle {\widetilde {W}}_{t}=W_{t}-\left[W,X\right]_{t}}$ est brownien sous Q.

La continuité de ${\displaystyle {\tilde {W}}_{t}}$ est triviale; selon le théorème de Girsanov, c'est une martingale locale sous Q, or :

${\displaystyle \left[{\widetilde {W}}\right]_{t}=\left[W\right]_{t}=t}$

Ce qui correspond à la caractérisation de Lévy du mouvement brownien sous Q.

Commentaires

• Dans de nombreuses applications usuelles, le processus X est défini par

${\displaystyle X_{t}=\int _{0}^{t}Y_{s}\,dW_{s}.}$

Pour un processus X de cette forme, une condition suffisante pour que l'exponentielle stochastique Z soit une martingale est la condition de Novikov :

${\displaystyle E_{P}\left[\exp \left(1/2\int _{0}^{T}Y_{s}^{2}\,ds\right)\right]<\infty .}$

Application à la finance

Ce théorème peut être utilisé pour trouver l'unique probabilité risque neutre dans le modèle de Black-Scholes.

Ainsi, si un actif suit le processus de diffusion vérifiant :

${\displaystyle {\frac {dS}{S}}=\mu dt+\sigma dW_{t}}$ où ${\displaystyle W_{t}}$ est un P-mouvement brownien.

En effectuant le changement de probabilité suivant :

${\displaystyle \left.{\frac {dQ}{dP}}\right|_{{\mathcal {F}}_{t}}=\exp \left(\int _{0}^{t}{\frac {r-\mu }{\sigma }}\,dW_{s}-{\frac {1}{2}}\int _{0}^{t}\left({\frac {r-\mu }{\sigma }}\right)^{2}ds\right).}$

On obtient une diffusion vérifiant :

${\displaystyle {\frac {dS}{S}}=rdt+\sigma d{\tilde {W_{t}}}}$

Où ${\displaystyle {\tilde {W_{t}}}}$ est un Q-mouvement brownien.

Si on note ${\displaystyle {\tilde {S}}}$ la valeur actualisée de ${\displaystyle S}$, on a :

${\displaystyle {\frac {d{\tilde {S}}}{\tilde {S}}}=\sigma d{\tilde {W}}_{t}}$

Sous la probabilité Q la valeur de notre actif réactualisée est une martingale.

Autre énoncé du théorème

On donne ici un énoncé plus simple du théorème, Soit ${\displaystyle \{\Omega ,{\mathcal {F}},P,\{{\mathcal {F}}_{t}\}_{0\leq t\leq T}\}}$ un espace probabilisé, muni de la filtration naturelle par rapport au processus de Wiener standard ${\displaystyle (W_{t};t\in [0;T])}$. Soit ${\displaystyle (Y_{t})_{0\leq t\leq T}}$ un processus adapté tel que :${\displaystyle \int _{0}^{T}Y_{s}^{2}\,\mathrm {d} s<\infty }$ P-f.s. et tel que le processus ${\displaystyle (Z_{t})_{0\leq t\leq T}}$ défini par:

${\displaystyle Z_{t}=\exp \left(\int _{0}^{t}Y_{s}\mathrm {d} W_{s}-{\frac {1}{2}}\int _{0}^{t}Y_{s}^{2}\mathrm {d} s\right)}$

soit une martingale.

Alors sous la probabilité ${\displaystyle P^{(Z)}}$ de densité ${\displaystyle Z_{T}}$ par rapport à P, le processus ${\displaystyle ({\tilde {W}}_{t})_{0\leq t\leq T}}$ défini par ${\displaystyle {\tilde {W}}_{t}=W_{t}-\int _{0}^{t}Y_{s}\mathrm {d} s}$ est un processus de Wiener standard.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Girsanov theorem » (voir la liste des auteurs).
• C. Dellacherie et P.-A. Meyer, Probabilités et potentiel – Théorie des martingales, Hermann, 1980, chap. VII
• E. Lenglart, « Transformation des Martingales locales par changement absolument continu de probabilities », dans Zeitschrift für Wahrscheinlichkeit, vol. 39, 1977, p. 65-70

Voir aussi

Articles connexes

• Théorème de Cameron-Martin (en)
• Igor Girsanov (en)
• Norbert Wiener
• Johann Radon

Liens externes

• (en) Alan Bain, Stochastic Calculus (contient une preuve du théorème de Girsanov)
• (en) Denis Papaioannou, Applied Multidimensional Girsanov Theorem (contient des applications du théorème de Girsanov en finance)

• Portail des probabilités et de la statistique