Harmonikus oszcillátor

A harmonikus rezgőmozgást végző tömegpontot nevezzük harmonikus oszcillátornak.

Egydimenziós (lineáris) harmonikus oszcillátor

Az m tömegű egydimenziós harmonikus oszcillátorra ${\displaystyle F=-kx}$ rugalmas erő hat, ahol k pozitív állandó. Mivel ${\displaystyle F_{x}=-{\frac {\partial V}{\partial x}}}$, a potenciális energia: ${\displaystyle V(x)={\frac {1}{2}}kx^{2}}$. Ha a potenciális energiát (${\displaystyle V(x)}$) a hely (x) függvényében ábrázoljuk, parabolát kapunk.

Schrödinger-egyenlet és megoldása

A harmonikus oszcillátor Schrödinger-egyenlete: ${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+{\frac {1}{2}}kx^{2}\psi =E\psi }$

A Schrödinger-egyenlettel meghatározhatóak a lehetséges energia-sajátértékek (${\displaystyle E_{n}}$), és a hozzájuk tartozó sajátfüggvények (${\displaystyle \psi _{n}}$). Az egyenletet a Sommerfeld-féle polinom módszerrel lehet megoldani.

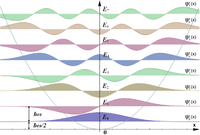
Az energia lehetséges értékei a sajátértékek: ${\displaystyle E_{n}=\left(n+{\frac {1}{2}}\right)\hbar \omega =\left(n+{\frac {1}{2}}\right)h\nu }$, ahol ${\displaystyle \omega =2\pi \nu ={\sqrt {\frac {k}{m}}}}$ körfrekvencia, és n=0,1,2,... nemnegatív egész szám. Ezzel a sajátértékek teljes rendszerét megkaptuk. Az oszcillátor energia-sajátértékei tehát nem vesznek fel tetszőleges értékeket, hanem ${\displaystyle h\nu }$ kvantum egész számú többszörösei.

Az ${\displaystyle n=0}$-hoz tartozó ${\displaystyle E_{0}={\frac {h\nu }{2}}}$ sajátértéket az oszcillátor zéruspont-energiájának nevezzük.

A szomszédos energiaszintek közti különbség: ${\displaystyle E_{n}-E_{n-1}=h\nu }$

AZ ${\displaystyle E_{n}}$ sajátértékhez tartozó sajátfüggvény: ${\displaystyle \psi _{n}\sim H_{n}\left({\frac {x}{a}}\right)e^{-{\frac {x^{2}}{2a^{2}}}}}$, ahol ${\displaystyle a^{4}={\frac {\hbar ^{2}}{mc}}}$, és ${\displaystyle H_{n}}$ az n-dik Hermite-polinom.

Az arányossági tényező egy normáló tag, mivel ${\displaystyle |\psi |^{2}=1}$-nek teljesülnie kell.

Alkalmazás

• Kétatomos molekulák vibrációs színképének értelmezése

  A kétatomos molekulákban az atomokat közelítőleg rugalmas erők tartják egymás közelében. A molekula ezek hatására rezgéseket végez, amelyek lehetséges energiaértékeit a fenti energiasajátértékek adják meg.

• Szilárd testek Einstein-modellje

  A modellben a szilárd testet úgy képzeljük el, hogy az atomjai a kristályrács rácspontjaiban helyezkednek el, és egyensúlyi helyzetük körül kis amplitúdóval rezegnek. A test minden atomja azonos amplitúdóval rezeg, és a köztük lévő kölcsönhatástól eltekintünk. Ekkor az atomokat elemi oszcillátorokként vizsgálhatjuk, így jó közelítéssel meghatározhatjuk a szilárd anyag moláris hőkapacitásának értékét.

Háromdimenziós harmonikus oszcillátor

Ez a szakasz egyelőre üres vagy erősen hiányos. Segíts te is a kibővítésében!

Az energia lehetséges értékei: ${\displaystyle E_{n1,n2,n3}\sim \left(n_{1}+n_{2}+n_{3}+{\frac {3}{2}}\right)}$

Lásd még

• Kvantummechanika
• Sajátvektor és sajátérték
• Schrödinger-egyenlet
• Valószínűségi amplitúdó

Források

• Marx György: Kvantummechanika (Műszaki Kiadó, Budapest)
• Nagy Károly: Kvantummechanika (Nemzeti Tankönyvkiadó, Budapest ISBN 963-19-1127-6)