Funzione di densità di probabilità

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

In matematica, una funzione di densità di probabilità (o PDF dall'inglese probability density function) è l'analogo della funzione di probabilità di una variabile casuale ma con la condizione che la variabile casuale ${\displaystyle X}$ sia continua, cioè l'insieme dei possibili valori che ha la potenza del continuo. Essa descrive la "densità" di probabilità in ogni punto nello spazio campionario.

Definizione

La funzione di densità di probabilità di una variabile casuale ${\displaystyle X}$ è un'applicazione ${\displaystyle p_{X}(x)}$ non negativa integrabile secondo Lebesgue e reale di variabile reale tale che la probabilità dell'insieme A sia data da

${\displaystyle P(X\in A)=\int _{A}p_{X}(x)\,\mathrm {d} x}$

per tutti i sottinsiemi A dello spazio campionario. Intuitivamente, se una distribuzione di probabilità ha densità ${\displaystyle p_{X}(x)}$, allora l'intervallo ${\displaystyle [x,x+\mathrm {d} x]}$ ha probabilità ${\displaystyle p_{X}(x)\,\mathrm {d} x}$. Da ciò deriva che la funzione ${\displaystyle p_{X}(x)}$ è un'applicazione definita come

${\displaystyle p_{X}({\bar {x}}):{\bar {x}}\mapsto \lim _{\mathrm {d} x\to 0}{\frac {P(x<{\bar {x}}<x+\mathrm {d} x)}{\mathrm {d} x}}}$

Assumendo ${\displaystyle x\equiv {\bar {x}}}$, ciò corrisponde al limite della probabilità che ${\displaystyle {\bar {x}}}$ si trovi nell'intervallo ${\displaystyle [x,x+\mathrm {d} x]}$ per ${\displaystyle \mathrm {d} x}$ che tende a zero. Di cui il nome di funzione di 'densità', in quanto essa rappresenta il rapporto tra una probabilità e un'ampiezza.

Per la condizione di normalizzazione l'integrale su tutto lo spazio di ${\displaystyle p_{X}(x)}$ deve essere 1. Di conseguenza ogni funzione non negativa, integrabile secondo Lebesgue, con integrale su tutto lo spazio uguale a 1, è la funzione densità di probabilità di una ben definita distribuzione di probabilità. Una variabile casuale che possiede densità si dice "variabile casuale continua".

Per le variabili casuali multivariate (o vettoriali) la trattazione formale è assolutamente identica: ${\displaystyle (X_{1},\ldots ,X_{n})}$ si dice assolutamente continua se esiste una funzione a valori reali definita in ${\displaystyle \mathbb {R} ^{n}}$, detta densità congiunta, tale che per ogni sottoinsieme A dello spazio campionario

${\displaystyle P(X\in A)=\int _{A}p_{X_{1},\ldots ,X_{n}}(x_{1},\ldots ,x_{n})\,\mathrm {d} x_{1}\ldots \mathrm {d} x_{n}}$

Essa conserva tutte le proprietà di una densità scalare: è una funzione non negativa a integrale unitario su tutto lo spazio. Una proprietà importante è che se ${\displaystyle (X_{1},\ldots ,X_{n})}$ è assolutamente continua allora lo è ogni sua componente; il viceversa invece non vale. La densità di una componente, detta densità marginale, si ottiene con un ragionamento analogo al teorema della probabilità assoluta, cioè fissando l'insieme di suoi valori di cui si vuole determinare la probabilità e lasciando libere di variare tutte le altre componenti. Infatti (nel caso bivariato per semplicità) l'evento ${\displaystyle (X\in A)}$ è l'evento ${\displaystyle (X\in A,Y\in \mathbb {R} )}$, dunque

${\displaystyle P(X\in A)=\int _{A\times \mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} x\,\mathrm {d} y=\int _{A}\left(\int _{\mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} y\right)\mathrm {d} x}$

utilizzando il teorema di Fubini. La densità marginale di ${\displaystyle X}$ è data dunque da

${\displaystyle p_{X}(x)=\int _{\mathbb {R} }p_{X,Y}(x,y)\,\mathrm {d} y}$.

Esempi

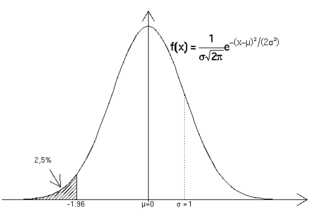
La funzione di densità della variabile casuale normale di media 0 e varianza 1 (detta normale standard), di cui a destra è riportato il grafico e l'espressione analitica della corrispondente densità nel caso generico (media ${\displaystyle \mu }$ e varianza ${\displaystyle \sigma ^{2}}$).

Un altro esempio può essere dato dalla densità di probabilità uniforme su un segmento (0,1). Si può verificare immediatamente che è densità di probabilità facendo l'integrale tra (0,1).

Voci correlate

• Funzione di ripartizione
• Funzione di probabilità
• Funzione caratteristica (teoria della probabilità)
• Variabile casuale
• Teoria della probabilità
• Statistica
• Integrale
• Percentile
• Quantile

Collegamenti esterni

• (EN) Eric W. Weisstein, Funzione di densità di probabilità, su MathWorld, Wolfram Research.
• (EN) IUPAC Gold Book, "probability density", su goldbook.iupac.org.

V · D · M Probabilità
Teoria della probabilità	Evento · Spazio campionario · Indipendenza stocastica · Probabilità condizionata · Teorema di Bayes · Disuguaglianza di Čebyšëv · Disuguaglianza di Markov
Variabili casuali	Misura di probabilità · Funzione di densità di probabilità · Funzione di ripartizione · Funzione caratteristica · Funzione generatrice dei momenti · Convergenza di variabili casuali
Distribuzioni di probabilità univariate	Distribuzioni discrete Uniforme discreta · Binomiale (Bernoulliana) · Degenere · Ipergeometrica · Di Pascal · Geometrica · Poissoniana Distribuzioni continue Uniforme continua · Normale · Esponenziale · Beta · Gamma · t di Student · di Cauchy · Chi Quadrato
Distribuzioni di probabilità multivariate	Multinomiale · Normale multivariata · Wishart · Dirichlet
Processi stocastici	Matrice stocastica · Processo markoviano · Passeggiata aleatoria · Martingala · Moto browniano · Integrale di Itō · Equazione differenziale stocastica
Discipline connesse	Combinatoria · Statistica

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica