Logaritm

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-04) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan.

Matematiska operationer v • r
Addition (+)
term + term addend + addend	=	summa
Subtraktion (−)
term − term minuend − subtrahend	=	differens
Multiplikation (× eller ·)
faktor × faktor multiplikator × multiplikand	=	produkt
Division (÷ eller /)
täljare / nämnare dividend / divisor	=	kvot
Moduloräkning (mod)
dividend mod divisor	=	rest
Exponentiering (^)
basexponent	=	potens
n:te roten (√)
grad √radikand	=	rot
Logaritm (log)
logbas(potens)	=	exponent

Logaritmen är inom matematiken den inversa funktionen till exponentiering. Logaritmen för ett tal a är den exponent x till vilket ett givet tal, med basen b, måste upphöjas för att anta värdet a:

${\displaystyle \ a=b^{x}}$

Logaritmer kan vara ett hjälpmedel, i synnerhet vid manuella beräkningar med stora antal av tal, genom att multiplikationer och divisioner kan omvandlas till additioner respektive subtraktioner.

Logaritmernas uppfinnare anses vara skotten John Napier (1600-talet).

Reella logaritmen

För reella tal måste gälla att a > 0 och b > 0 för att logaritmen ska kunna beräknas. Logaritmen x kan anta godtyckliga värden. I uttrycket a = b^x kallas x logaritmen av a i basen b och skrivs

${\displaystyle \ x=\log _{b}a\quad }$ där alltså ${\displaystyle a,b\in \mathbb {R} }$ och ${\displaystyle a,b>0}$

Tiologaritmen eller briggska logaritmen

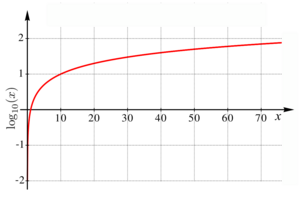
Ett praktiskt val av logaritmbas vid användning av den decimala notationen är den briggska logaritmen (10-logaritmen utvecklad av Henry Briggs). Den briggska logaritmen för ett tal a är den exponent x till vilken 10 skall upphöjas för att bilda talet a:

${\displaystyle 10^{x}=a\quad \Leftrightarrow \quad x=\log _{10}a}$

Andra beteckningssätt för log₁₀ a är log a och lg a.

Naturliga logaritmen (logaritmus naturalis)

En speciell bas är e (Eulers tal). Beteckningen för log_e a, den naturliga logaritmen av a, är ln a.

Detta ger sambanden

${\displaystyle a=\mathrm {e} ^{x}\Leftrightarrow x=\ln a.}$

En viktig anledning till att denna logaritm används är att den är den inversa funktionen till exponentialfunktionen e^x.

En intressant egenskap hos den naturliga logaritmfunktionen är att dess derivata är 1/x, vilket gör att den fyller ut en lucka bland de primitiva funktionerna till potensfunktioner:

${\displaystyle \int x^{n}dx=}$${\displaystyle \left\{{\begin{matrix}{\frac {x^{n+1}}{n+1}}+C&{\mbox{om }}n\neq -1\\\ln x+C&{\mbox{om }}n=-1\end{matrix}}\right.}$

n = -1 leder till division med noll, vilket är otillåtet. För varje tal nära -1 kommer "första primitiva funktionen" att vara godtyckligt nära ln x. Därför kan logaritmen ses som en kontinuerlig utvidgning av polynomen, ett faktum som även kan motiveras genom att betrakta vissa speciella gränsfall av interpolationspolynomen (kanske enklast via Newtons interpolationspolynom).

Se även definitionen av talet e.

Komplexa logaritmen

Den flervärda komplexa logaritmen log definieras som urbilden till exponentialfunktionen, det vill säga

${\displaystyle \log :\mathbb {C} \to 2^{\mathbb {C} },\ z\mapsto \{w\in \mathbb {C} :\exp w=z\}}$

Vilket också kan uttryckas som

${\displaystyle \ \log z=\ln |z|+i*(arg(z)+n*2\pi )}$

där + innebär addition av vektormängder och arg är argumentsfunktionen. Den komplexa logaritmen uppfyller de flesta räkneregler för den reella logaritmen; problem kan uppstå om exempelvis summan av två argument hamnar utanför grenen. Man kan studera en gren av logaritmen, som då blir en envärd funktion. För principalgrenen Log används principalgrenen av argumentsfunktionen, dvs

${\displaystyle \mathrm {Im} \ \mathrm {Log} \ z\in (-\pi ,\pi )}$.

Diskreta logaritmen

På samma sätt som ovan kan man definiera en logaritm i en godtycklig ändlig kropp. Det är då ett väldefinierat begrepp eftersom en kropp under multiplikation (andra kompositionsoperatorn) är isomorf med en cyklisk delgrupp. Som bas för logaritmen väljer man en generator för denna cykliska grupp. Utvidgningen är helt analog med reella logaritmer. Skillnaden mellan reella logaritmer och diskreta logaritmer är att den diskreta logaritmen alltid blir ett heltal. I övrigt har diskreta och reella logaritmen likartade lagar och följer ungefärligen samma teori.

Till skillnad från vanliga (reella) logaritmer är det generellt sett svårt att hitta logaritmen för ett givet tal. Man kallar detta diskreta logaritmproblemet. Faktum är att det är så svårt, att man använder denna svårighet för att konstruera säker kryptering. Poängen är att det är lätt att verifiera en föreslagen logaritm, men svårt att finna den. Metoden påminner om hur man i krypteringsalgoritmer utnyttjar problemet med finna primtalsfaktorisering av stora tal.

Derivata

Derivatan av en logaritmfunktion

${\displaystyle y=\log _{b}\,x}$

är

${\displaystyle {\frac {dy}{dx}}={\frac {1}{x\ln b}}}$

Speciellt är

${\displaystyle {\frac {d}{dx}}\ln x={\frac {1}{x}}}$

Identiteter

• ${\displaystyle \ \log _{b}a=x\leftrightarrow b^{x}=a}$

• ${\displaystyle \ b^{\log _{b}a}=a}$

• ${\displaystyle \ a^{x}=\mathrm {e} ^{x\ln a}}$

• ${\displaystyle \ \log _{a}(xy)=\log _{a}(x)\,+\,\log _{a}(y)}$

• ${\displaystyle \ \log {}(a^{p})=p\log {}(a)}$

• ${\displaystyle \ \log _{a}\left({\frac {x}{y}}\right)=\log _{a}(x)-\log _{a}(y)}$

• ${\displaystyle \ \log _{a}(x^{p})=p\,\log _{a}(x)}$

• ${\displaystyle \ \log _{a}x={\frac {\log _{b}x}{\log _{b}a}}={\frac {\ln x}{\ln a}}}$

• ${\displaystyle \ \log {}({\sqrt[{p}]{a}})={1 \over p}\log(a)}$

Exempel

Logaritmernas främsta ursprungliga nytta var att ersätta långa sekvenser av multiplikationer med mindre tidskrävande sekvenser av additioner.

Antag att produkten 217 · 596 skall beräknas utan användande av multiplikation. Enligt logaritmlagarna är summan av faktorernas logaritmer lika med logaritmen för produkten:

${\displaystyle \log a+\log b=\log ab\Rightarrow }$

${\displaystyle \log 217+\log 596=2.33646+2.77525=5.11171}$

Med hjälp av en tabell går det att bestämma vilket tal som har logaritmen 5.11171:

${\displaystyle \log x=5.11171\quad \Rightarrow {\text{tabelluppslagning}}\Rightarrow \quad x=129332}$

Exempel (reella logaritmen)

Logaritmerna kan användas för att lösa vissa ekvationer. Antag att ekvationen

${\displaystyle 7^{x}=1234}$

skall lösas med hjälp av logaritmer. Bilda 10-logaritmen av båda sidor:

${\displaystyle \log 7^{x}=\log 1234}$

Utnyttja en av logaritmlagarna:

${\displaystyle x\cdot \log 7=\log 1234}$

Beräkna värdet av x på miniräknaren:

${\displaystyle x={\cfrac {\log 1234}{\log 7}}=3.65794}$

Exempel (diskreta logaritmen)

Det går att använda diskreta logaritmer för att lösa ekvationer i godtyckliga kroppar. Här visas hur man bestämmer diskreta logaritmer i en given kropp.

I exemplet kommer vi att betrakta galoiskroppen av ordning 27, GF(3³). Den genereras av ett kubiskt irreducibelt polynom över ℤ₃ via Kroneckers konstruktion. Ett sådant irreducibelt polynom är x³ + 2x + 1 vilket inses genom att manuellt undersöka de möjliga rötterna. Därmed har vi en kropp

${\displaystyle \mathbb {Z} _{3}[x]/<x^{3}+2x+1>}$

med 27 element som kommer att vara isomorf med GF(27). I den går det nu att beräkna diskreta logaritmer.

Låt oss här återge stegen vi tagit lite mer detaljerat. Vi har hittat ett irreducibelt polynom över ℤ₃. Då kommer

${\displaystyle \mathbb {Z} _{3}[x]/<x^{3}+2x+1>}$

att bli en kropp, som genereras av ett principalt ideal.

Detta förklaras genom att ℤ₃ är en kropp och därför är varje ideal i ℤ₃[x] principalt och genom att polynomet x³ + 2x + 1 är irreducibelt. Därför är < x³ + 2x + 1 > ett maximalt ideal. Och därför är kvotringen

${\displaystyle \mathbb {Z} _{3}[x]/<x^{3}+2x+1>}$

inte bara en kvotring, utan en kropp.

Låt oss ta reda på vad elementet/sidoklassen x² + 1 har som diskret logaritm. Genom att successivt beräkna potenser xⁿ där ${\displaystyle n=0,1,\dots ,26}$ fås att första gången xⁿ = x² + 1 är när n = 21:

${\displaystyle \ n=0,\ x^{0}=1}$

${\displaystyle \ n=1,\ x^{1}=x}$

${\displaystyle \ n=2,\ x^{2}=x^{2}}$

${\displaystyle \ n=3,\ x^{3}=x+2}$

${\displaystyle \ n=4,\ x^{4}=x^{2}+2x}$

${\displaystyle \ n=5,\ x^{5}=2x^{2}+x+2}$

${\displaystyle \ n=6,\ x^{6}=x^{2}+x+1}$

${\displaystyle \ \ldots }$

${\displaystyle \ n=21,\ x^{21}=x^{2}+1}$

Därför är log_x(x² + 1) = 21. Notera att det var nödvändigt att gå igenom ett stort antal exponenter n = 0, 1, … för att hitta den vi sökte. Det finns bättre algoritmer för att hitta diskreta logaritmen. Men även med dessa är det generellt sett en tidsödande process, eftersom man kan konstruera kroppar av mycket hög ordning.

Antilogaritm

Antilogaritmen är ett annat namn för potens. Även om termen visserligen används är det ett inte helt lyckat bruk, eftersom potens är konventionen.

Se även

• Karakteristika
• Mantissa
• Logaritmisk skala

Externa länkar

• Wikimedia Commons har media som rör Logaritm.
  Bilder & media

Auktoritetsdata • LCCN: sh85078091 • GND: 4168047-9 • BNF: cb11941516p (data) • NDL: 00572566 • BNE: XX527539