Funció d'error

Funció d'error
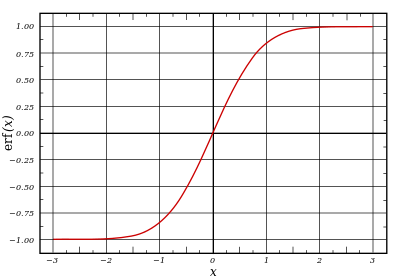Gràfic de la funció d'error
Informació general
Definició general	${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t}$
Camps d'aplicació	Probabilitat, termodinàmica
Domini, codomini i imatge
Domini	${\displaystyle \mathbb {C} }$
Imatge	${\displaystyle \left(-1,1\right)}$
Característiques bàsiques
Paritat	Senar
Característiques específiques
Arrel	0
Derivada	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}}$
Primitiva	${\displaystyle \int \operatorname {erf} z\,dz=z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}+C}$
Definició amb sèries
Sèrie de Taylor	${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}}$

En matemàtiques, la funció d'error (també anomenada funció d'error de Gauss), sovint denotada per erf, és una funció complexa d'una variable complexa definida com: ^[1]

${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t.}$

Aquesta integral és una funció sigmoide especial (no elemental) que apareix sovint en equacions de probabilitat, estadístiques i en derivades parcials. En moltes d'aquestes aplicacions, l'argument de la funció és un nombre real. Si l'argument de la funció és real, llavors el valor de la funció també és real.^[2]

En estadística, per a valors no negatius de x, la funció d'error té la següent interpretació: per a una variable aleatòria Y que té una distribució normal amb una mitjana μ igual a 0 i una desviació estàndard σ igual a ${\displaystyle 1/{\sqrt {2}}}$, erf(x) és la probabilitat que Y caigui en el rang [−x, x].

• 
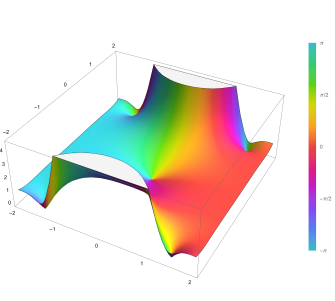  Gràfic de la funció d'error Erf(z) en el pla complex de -2-2i a 2+2i amb colors creats amb la funció de Mathematica 13.1 ComplexPlot3D.

Dues funcions estretament relacionades són la funció d'error complementària (erfc) definida com

${\displaystyle \operatorname {erfc} z=1-\operatorname {erf} z,}$

i la funció d'error imaginari (erfi) definida com

${\displaystyle \operatorname {erfi} z=-i\operatorname {erf} iz,}$

on i és la unitat imaginària.^[3]

El nom "funció d'error" i la seva abreviatura erf van ser proposats per JWL Glaisher l'any 1871 a causa de la seva connexió amb "la teoria de la probabilitat, i sobretot la teoria dels errors".^[4] El complement de la funció d'error també va ser discutit per Glaisher en una publicació separada el mateix any.^[5] Per a la "llei de la facilitat" dels errors la densitat dels quals ve donada per

${\displaystyle f(x)=\left({\frac {c}{\pi }}\right)^{\frac {1}{2}}e^{-cx^{2}}}$

Aplicacions

Quan els resultats d'una sèrie de mesures es descriuen mitjançant una distribució normal amb desviació estàndard σ i valor esperat 0, llavors ${\displaystyle erf(a/\sigma /{\sqrt {2}})}$ és la probabilitat que l'error d'una sola mesura estigui entre −a i +a, per a a positiva. Això és útil, per exemple, per determinar la taxa d'error de bits d'un sistema de comunicació digital.

Referències