Model Booleà Estès

El Model Booleà Estès és una variació del Model Booleà, que permet un maneig més flexible dels termes de la consulta i una revisió dels resultats. El Model Booleà Estès va ser presentat en un article de Communications of the ACM en l'any 1983, per Gerard Salton, Edward A. Fox i Harry Wu, amb el propòsit superar els desavantatges del Model Booleà que ha estat utilitzat en recuperació d'informació.

El Model Booleà no considera els pesos dels termes en les consultes i el conjunt resposta d'una consulta booleana és sovint massa petita o massa gran. La sol·licitud de recuperació booleana clàssica determina quins elements han d'aparèixer en els resultats de la consulta. La sol·licitud divideix els documents en dos grups: aquells documents no compleixen amb la sol·licitud i els que la compleixen. Això porta dos problemes:

1. Un document que no conté un terme requerit no es troba. No obstant això, el document podria ser rellevant. Potser el terme requerit simplement apareix amb un nom diferent (sinonímia). Altres termes de consulta poden ser nombrosos.
2. Els documents que coincideixen amb els criteris de la consulta, no poden ser ordenats per rellevància.

La idea del model estès és fer ús de la correspondència parcial i els pesos dels termes del Model d'Espai Vectorial, combinant-los amb les propietats de l'àlgebra booleana, intentant abordar aquests problemes amb la naturalesa binària del àlgebra booleana (veritat - fals); els valors es defineixen matemàticament en un interval [0,1], amb 0 és «fals» i 1 és «veritat». D'aquesta manera, un document pot ser una mica rellevant si conté alguns termes de la consulta i pot ser obtingut com a resposta, mentre que en el Model Booleà això no passa.^[1]

Així, el Model Booleà Estès pot ser considerat com una generalització dels models booleà i vectorial. A més, la investigació ha demostrat millores en l'efectivitat respecte al processament de consultes del model booleà. Altres investigacions han mostrat que la retroalimentació i l'expansió de consultes poden ser adaptades al processament de consultes del Model Booleà Estès.

Definicions

En el Model Booleà Estès, un document es representa per un vector, la 4-tupla (T , Q , D , rang (.,.)), igual que en el Model Vectorial. Cada component correspon a un terme associat al document:

• T = { t_i | i = 1, ..., n}: conjunt d'índex de termes, documents i descripcions de consultes.
• Q = { q_j | i = 1, ...}: conjunt de totes les consultes permeses.
• D = { d_k | k = 1, ..., m}: quantitat d'aquest document. En els models booleanes estesos cada terme té t_ki d'un document d_k un pes w_ki ∈ [0,1], representant la importància del terme en el document. D'aquesta manera, un document d_k té l'estructura d_k = (( t_k1 , w_k1 ), ..., ( t_kN , w_kn )).
• rang (..): funció de la classificació, que descriu la similitud d'un document amb una consulta. En general, es defineix per: rang (d_k , q_j): D x Q → [0,1]: (d_k , q_j | → rang (d_k, q_j) ∈ [0,1].

En la funció de classificació es descriuen les diferents classes del Model Booleà Estès; en tots els models es poden distingir els operadors lògics AND i OR en la consulta.

El pes del terme ${\displaystyle K_{x}}$ associat al document ${\displaystyle d_{j}}$ es mesura per la seva freqüència de terme normalitzada i pot definir-se com:

${\displaystyle w_{x,j}=f_{x,j}*{\frac {Idf_{x}}{max_{i}Idf_{x}}}}$

on ${\displaystyle Idf_{x}}$ és la freqüència inversa de document.

El vector de pesos associat al document ${\displaystyle d_{j}}$ pot ser representat com:

${\displaystyle \mathbf {v} _{d_{j}}=[w_{1,j},w_{2,j},\ldots ,w_{i,j}]}$

Exemple en 2 dimensions

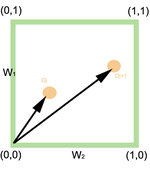
Considerant l'espai compost pels dos termes ${\displaystyle K_{x}}$ y ${\displaystyle K_{y}}$, els pesos corresponents són ${\displaystyle w_{1}}$ i ${\displaystyle w_{2}}$.^[2] Així, per a la consulta${\displaystyle q_{or}=K_{x}\lor K_{y}}$, podem calcular la similitud amb la següent fórmula:

${\displaystyle sim(q_{or},d)={\sqrt {\frac {w_{1}^{2}+w_{2}^{2}}{2}}}}$

Per a la consulta ${\displaystyle q_{and}=K_{x}\land K_{y}}$, podem fer servir:

${\displaystyle sim(q_{and},d)=1-{\sqrt {\frac {(1-w_{1})^{2}+(1-w_{2})^{2}}{2}}}}$

Generalització de la idea

Podem generalitzar l'exemple anterior en 2 dimensions del Model Booleà Estès a l'espai t-dimensional usant la distància Euclidiana.

Això pot fer-se usant Norma-P, que estén la noció de distància per incloure p-distàncies, on ${\displaystyle 1\leq p\leq \infty }$ és un nou paràmetre.

• Una consulta conjuntiva general està donada per:

${\displaystyle q_{or}=k_{1}\lor ^{p}k_{2}\lor ^{p}....\lor ^{p}k_{t}}$

La similitud de la consulta ${\displaystyle q_{or}}$ i el document ${\displaystyle d_{j}}$ pot definir-se com:

${\displaystyle sim(q_{or},d_{j})={\sqrt[{p}]{\frac {w_{1}^{p}+w_{2}^{p}+....+w_{t}^{p}}{t}}}}$

• Una consulta disjuntiva general està donada per:

${\displaystyle q_{and}=k_{1}\land ^{p}k_{2}\land ^{p}....\land ^{p}k_{t}}$

La similitud de la consulta ${\displaystyle q_{and}}$ i el document ${\displaystyle d_{j}}$ pot definir-se com:

${\displaystyle sim(q_{and},d_{j})=1-{\sqrt[{p}]{\frac {(1-w_{1})^{p}+(1-w_{2})^{p}+....+(1-w_{t})^{p}}{t}}}}$

Exemples

Penseu en la consulta ${\displaystyle q=(K_{1}\land K_{2})\lor K_{3}}$. La similitud entre la consulta ${\displaystyle q}$ i el document ${\displaystyle d}$ pot calcular-se usant la fórmula:

${\displaystyle sim(q,d)={\sqrt[{p}]{\frac {(1-{\sqrt[{p}]{({\frac {(1-w_{1})^{p}+(1-w_{2})^{p}}{2}}}}))^{p}+w_{3}^{p}}{2}}}}$

Models booleans avançats sense pesos de consulta

En aquesta classe de models cada consulta es representa com una combinació dels termes d'índex i els operadors lògics AND, OR, NOT, entre la possible utilització de qualsevol expressió entre parèntesis. Es creu que tots els termes tenen el mateix significat, que està representat per la falta de pesos termini en la consulta. Els següents models booleans estesos es poden distingir:

Model de conjunts difusos simples (Buell 1981, Bookstein 1980, Radecki 1979)

rang (d_k, t₁ AND t₂) = MIN {w_k1, w_k2}

rang (d_k, t₁ OR t₂) = MAX {w_k1, w_k2}

Aquest model simple té la limitació que només es pot avaluar dos termes, en contraposició als següents models que poden gestionar molts termes arbitraris.

Model Waller-Kraft (Waller i Kraft 1979)

rang (d_k, t₁ AND ... AND t_n) = (1 - γ) · MIN {w_k1, ..., w_kn} + γ · MAX {w_k1, ..., w_kn}, 0 ≤ γ ≤ 0,5

rang (d_k, t₁ OR ... OR t_n) = (1 - γ) · MIN {w_k1, ..., w_kn} + γ · MAX {w_k1, ..., w_kn}, 0,5 ≤ γ ≤ 1

Model Paice (Paice 1984)

En una operació inicial AND s'organitza els pesos w_ki en valors creixents, és a dir, w_k1 ≤ ... ≤ w_kN, i després es calcula

rang (d_k, t₁ AND ... AND t_n) = (∑_i=1ⁿ (r^i-1 · w_ki)) / (∑_i=1ⁿ r^i-1), 0 ≤ r ≤ 1

En una operació inicial OR s'organitza els pesos w_ki en valors descendent, és a dir, w_k1 ≥ ... ≥ w_kN, i després es calcula

rang (d_k, t₁ OR ... OR t_n) = (∑_i=1ⁿ (r^i-1 · w_ki)) / (∑_{i =1}ⁿ r^i-1), 0 ≤ r ≤ 1

Podel P-estàndard (Salton et al., 1983)

rang (d_k, t₁ AND ... AND t_n) = 1 - (1 / n · ∑_i=1ⁿ (1 - w_ki)^p)^1/p, 1 ≤ p <∞

rang (d_k, t₁ OR ... OR t_n) = 1 - (1 / n · ∑_i=1ⁿ (w_ki)^p)^1/p, 1 ≤ p <∞

Model infinit i un (Smith 1990)

rang (d_k, t₁ AND ... AND t_n) = γ · (1 - MAX {1 - w_k1, ..., 1 - w_kn}) + (1 - γ) · (1 / n · ∑_i=1ⁿ w_ki), 0 ≤ γ ≤ 1

rang (d_k, t1 OR ... OR t_n) = γ · MAX {w_k1, ..., w_kn} + (1 - γ) · (1 / n · ∑_i=1ⁿ w_ki), 0 ≤ γ ≤ 1

Els models booleans avançats amb pesos de consulta

L'efectivitat de la recuperació es pot augmentar per factors d'importància que s'assignen als termes en forma de pesos. Una consulta q_j d'aquesta manera crea una estructura anàloga a un document d_k amb tuples de termes i pesos. Són termes que no es produeixen en la consulta d'origen que codifica un pes zero, pel que cada consulta d'origen es poden codificar en una consulta que tingui en compte tots els termes que apareixen en T:

q_j = ((t_q(j)1, w_q(j)1), ..., (t_q(j)n, w_q(j)n)).

Els enfocaments rellevants de ponderació (veure Buell (1981)), reformulen les funcions de classificació tal que els pesos dels documents i les consultes es multipliquen, és a dir:

rang (d_k, (t_q(j), w_q(j))) = w_k · w_q(j)

Sota aquest supòsit, moltes de les funcions del Model Booleà Estès P-estàndard i del Model Booleà Estès infinit i un són capaces d'avaluar els pesos en els documents i una consulta:

Model P-estàndard amb pesos de consulta

rang (d_k (t_q(j)1, w_q(j)1) AND ... AND (t_q(j)n, w_q(j)n)) = 1 - ((∑_i=1ⁿ (1 - w_ki)^p · w_q(j)i^p) / (∑_i=1ⁿ w_ki^p))^1/p, 1 ≤ p <∞

rang (d_k (t_q(j)1, w_q(j)1) OR ... OR (t_q(j)n, w_q(j)n)) = 1 - ((∑_i=1ⁿ w_ki^p · w_q(j)i^p) / (∑_i=1ⁿ w_ki^p))^1/p, 1 ≤ p <∞

Model infinit i un amb pesos de consulta

rang (d_k, (t_q(j)1, w_q(j)1) AND ... AND (t_q(j)n, w_q(j)n)) = γ · (1 - ((MAX {(1 - w_k1) · w_q(j)1, ..., (1 - w_kn) · w_q(j)n}) / (MAX {w_q(j)1, ..., w_q(j)n})) + (1 - γ) · ((∑_i=1ⁿ (w_ki · w_q(j)i) / (∑_i=1ⁿ w_q(j)i)), 0 ≤ γ ≤ 1

rang (d_k, (t_q(j)1, w_q(j)1) OR ... OR (t_q(j)n, w_q(j)n)) = γ · (MAX {w_k1 · w_q(j)1, ..., w_kn · w_q(j)n}) / (MAX {w_q(j)1, ..., w_q(j)n}) + (1 - γ) · ((∑_i=1ⁿ (w_ki · w_q(j)i) / (∑_i=1ⁿ w_q(j)i)), 0 ≤ γ ≤ 1

Millores respecte al Model Booleà

Lee i Fox^[3] van comparar els models Booleà i Booleà Estès amb tres col·leccions de prova: CISI, CACM i INSPEC.

Utilitzant Norma-P es va obtenir una mitjana de millores en la precisió de 79%, 106% i 210% respecte al Model Booleà estàndard, per a les col·leccions CISI, CACM i INSPEC, respectivament.

El model de Norma-P és computacionalment costós pel nombre d'operacions d'exponenciació que requereix; però, aconsegueix resultats molt millors que el Model Booleà, i fins i tot que el Model Fuzzy. El Model Booleà estàndard és, però, el més eficient.

Referències

Bibliografia

• Buell, D.A.: A general model for query processing in information retrieval system. In: Information Processing and Management, 17, 1981, S. 249–262.
• Bookstein, A.: Fuzzy requests: an approach to weighted boolean searches. In: Journal of the American Society for Information Science, 31, 1980, S. 240–247.
• Fox, E.A.; Betrabet, S.; Koushik, M.; Lee, W.: Extended boolean models. In: Frankes, W.B.; Yates, R.B. (eds): Information Retrieval Data Structures and Algorithms. Prentice Hall, 1992, S. 393–418.
• Kim, M.H.; Lee, J.H.; Lee, Y.J.: Analysis of fuzzy operators for high quality information retrieval. In: Information Processing Letters, 46 (5), 1993, S. 251–256.
• Lee, J.H.; Kim, M.H.; Lee, Y.J.: Ranking documents in thesaurus-based boolean retrieval systems. In: Information Processing and Management, 30, 1994, S. 79–91.
• Lee, J.H.; Kim, M.I.I.; Lee, Y.J.: Enhancing the fuzzy set model for high quality document rankings. In: Proceedings of the 19th Euromicro Conference.1992, S. 337–344.
• Lee, J.H.; Kim, W.Y.; Kim, M.H.; Lee, Y.J.: On the evaluation of boolean operators in the extended boolean retrieval framework. In: SIGIR 1993, 1993, S. 291–297.
• Lee, Joon Ho: Properties of extended Boolean models in information retrieval. In: Croft & Rijsbergen (1994): SIGIR 1994, S. 182–190.
• Paice, C.P.: Soft evaluation of boolean search queries in information retrieval systems. In: Information Technology: Research and Development, 3 (1), 1984, S. 33–42.
• Radecki, T.: Fuzzy set theoretical approach to document retrieval. In: Information Processing and Management, 15, 1979, S. 247–259.
• Sachs, W.M.: An approach to associative retrieval through the theory of fuzzy sets. In: Journal of the American Society for Information Science, 27, 1976, S. 85–87.
• Salton, G.; Fox, E.A.; Wu, H.: Extended boolean information retrieval. In: Communication of the ACM, 26(11), 1983, S. 1022–1036.
• Smith, M.E.: Aspekts of the p-norm model of information retrieval: syntactic query generation, efficiency, and theoretical properties. PhD thesis, Cornell University, 1990.
• Waller, W.G.; Kraft, D.H.: A mathematical Model for weighted Boolean retrieval systems. In: Information Processing and Management, 15, 1979, S. 235–245.

Vegeu també

• Recuperació d'informació