Spline

Un spline quadràtic compost per sis segments polinòmics. Entre el punt 0 i el punt 1 una recta. Entre el punt 1 i el punt 2 una paràbola amb segona derivada = 4. Entre el punt 2 i el punt 3 una paràbola amb segona derivada = -2. Entre el punt 3 i el punt 4 una recta. Entre punt 4 i el punt 5 una paràbola amb segona derivada = 6. Entre el punt 5 i el punt 6 una recta.
Un spline cúbic compost per set segments polinòmics.
La derivada segona del spline cúbic de dalt.

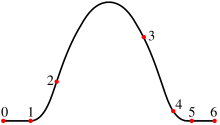
En matemàtiques, un spline (o traçador) és una funció polinòmica definida a trossos que interpola una sèrie de punts de forma que cada tros és un polinomi de grau n i a cada punt les derivades dels dos trossos que hi connecten tenen iguals les seves derivades fins a l'ordre n-1.

En problemes d'interpolació, la interpolació per splines es preferix sovint a la interpolació polinòmica perquè produeix resultats similars, fins i tot quan es fan servir polinomis de grau baix, mentre que evita el fenomen de Runge que apareix quan s'empren polnomis de graus alts

En infografia els splines són corbes emprades amb freqüència a causa de la simplicitat de la seva construcció, la facilitat i precisió en què es poden avaluar les funcions que els defineixen, i la seva capacitat d'aproximar formes complexes amb les tècniques d'ajust de corbes i de disseny interactiu de corbes.

El terme spline ve dels regles flexibles emprats pels constructors de vaixells i els dissenyadors industrials per dibuixar corbes.

Els splines que es fan servir més són els splines cúbics, és a dir d'ordre 3 en particular els B-splines 3 i els splines de Bézier cúbics. Són comuns, en particular, en interpolació per splines que simula la funció del regle flexible.

Definició

Un spline és una funció real polinòmica definida a trossos

S : [ a , b ] → R {\displaystyle S:[a,b]\to \mathbb {R} }

en un interval [a,b ] compost de k subintervals disjunts ordenats [ t i − 1 , t i ] {\displaystyle [t_{i-1},t_{i}]} amb

a = t 0 < t 1 < ⋯ < t k − 1 < t k = b {\displaystyle a=t_{0}<t_{1}<\cdots <t_{k-1}<t_{k}=b} .

La restricció de S a un interval i és un polinomi

P i : [ t i − 1 , t i ] → R {\displaystyle P_{i}:[t_{i-1},t_{i}]\to \mathbb {R} } ,

de manera que

S ( t ) = P 1 ( t ) ,  t 0 ≤ t < t 1 , {\displaystyle S(t)=P_{1}(t){\mbox{, }}t_{0}\leq t<t_{1},}
S ( t ) = P 2 ( t ) ,  t 1 ≤ t < t 2 , {\displaystyle S(t)=P_{2}(t){\mbox{, }}t_{1}\leq t<t_{2},}
⋮ {\displaystyle \vdots }
S ( t ) = P k ( t ) ,  t k − 1 ≤ t ≤ t k . {\displaystyle S(t)=P_{k}(t){\mbox{, }}t_{k-1}\leq t\leq t_{k}.}

L'ordre més alt dels polinomis P i ( t ) {\displaystyle P_{i}(t)} es diu que és l'ordre del spline S. Si tots els subintervals són de la mateixa llargada, el spline s'anomena uniforme i no-uniforme altrament.

La idea és escollir els polinomis d'una manera que garanteix suavitat suficient de S. Específicament, per un spline d'ordre n, a S sel li imposa que sigui contínuament diferenciable fins a l'ordre n-1 en els punts interiors t i {\displaystyle t_{i}} : per a tot i = 1 , … , k − 1 {\displaystyle i=1,\dots ,k-1} i tot j 0 ≤ j ≤ n − 1 {\displaystyle j\quad 0\leq j\leq n-1} ,

P i ( j ) ( t i ) = P i + 1 ( j ) ( t i ) {\displaystyle P_{i}^{(j)}(t_{i})=P_{i+1}^{(j)}(t_{i})} .

Obtenció d'un Spline Cúbic que interpola entre punts

Aquest és un dels usos més importants dels splines. L'algoritme per fer-ho es donarà a l'article Interpolació per splines

Exemples

L'spline d'Irwin-Hall en forma acampanada
La derivada segona del spline de dalt

Un exemple simple d'un spline quadràtic (un spline del grau 2) és

S ( t ) = { ( t + 1 ) 2 − 1 − 2 ≤ t < 0 1 − ( t − 1 ) 2 0 ≤ t ≤ 2 {\displaystyle S(t)={\begin{cases}(t+1)^{2}-1&-2\leq t<0\\1-(t-1)^{2}&0\leq t\leq 2\end{cases}}}

per al qual S ′ ( 0 ) = 2 {\displaystyle S'(0)=2} .

Un exemple simple d'un spline cúbic és

S ( t ) = | t | 3 {\displaystyle S(t)=\left|t\right|^{3}}

on

S ( t ) = { t 3 t ≥ 0 − t 3 t < 0 {\displaystyle S(t)={\begin{cases}t^{3}&t\geq 0\\-t^{3}&t<0\end{cases}}}

i

S ( 0 ) ′ =   0 {\displaystyle S(0)'=\ 0}

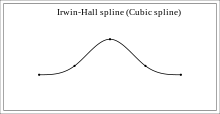
Un exemple d'utilitzar un s plinecúbic spline per crear una corba amb forma de campana són els polinomis d'Irwin-Hall:

f X ( x ) = { 1 4 ( x + 2 ) 3 − 2 ≤ x ≤ − 1 1 4 ( 3 | x | 3 − 6 x 2 + 4 ) − 1 ≤ x ≤ 1 1 4 ( 2 − x ) 3 1 ≤ x ≤ 2 {\displaystyle f_{X}(x)={\begin{cases}{\frac {1}{4}}(x+2)^{3}&-2\leq x\leq -1\\{\frac {1}{4}}\left(3|x|^{3}-6x^{2}+4\right)&-1\leq x\leq 1\\{\frac {1}{4}}(2-x)^{3}&1\leq x\leq 2\end{cases}}}

Història

Abans que s'utilitzessin ordinadors, els càlculs numèrics es feien a mà. S'utilitzaven funcions com la funció esglaonada però es preferien generalment polinomis. Amb l'adveniment d'ordinadors, els splines primer varen reemplaçar als polinomis en la interpolació, i després en la construcció de formes llises i flexibles en gràfics informàtics.[1]

S'accepta comunament que la primera referència matemàtica als splines és l'article 1946 de Schoenberg,[2] que és probablement el primer lloc on la paraula "spline" és utilitzada en la connexió amb, aproximació polinòmica a bocins contínuament derivable. Tanmateix, aquestes idees tenen les seves arrels a la indústria de construcció naval i aeronàutica. En el prefaci a Bartels et al.,[3] Robin Forrest descriu el "lofting", una tècnica utilitzada a la indústria aeronàutica britànica durant la Segona Guerra Mundial per construir plantilles per a avions fent passar bandes de fusta primes (anomenades "splines") a través dels punts fixats al terra d'unes grans sales de disseny, una tècnica presa en préstec del disseny de vaixells. Durant anys la pràctica de disseny de vaixells havia fet servir models per fer el disseny a petita escala. Llavors el disseny final es dibuixava en paper de gràfics i els punts clau de la trama es redibuixaven en paper de gràfic més gran a escala real. Les regles flexibles proporcionaven una interpolació dels punts clau a corbes llises. Les regles flexibles es mantenien a lloc en punts discrets i entre aquests punts implicava aplicar formes de mínima energia de deformació. Segons Forrest, una possible motivació per obtenir un model matemàtic per a aquest procés era la pèrdua potencial dels components de disseny crítics per a una aeronau sencera si la sala de disseny fos colpida per una bomba enemiga. Això va donar lloc al "conic lofting", que utilitzava seccions còniques per imitar la posició de la corba entre els punts. El "conic lofting" es va canviar pel que anomenem splines als primers anys de la dècada del 1960 basats en el treball de J. C. Ferguson[4] a Boeing i (una mica més tard) per M. A. Sabin a la British Aircraft Corporation.

L'ús de splines per al disseny de xassís d'automòbils sembla que té uns quants començaments independents. Citroën reclama l'honor a favor de Paul de Casteljau, Renault el reclama per Pierre Bézier, i General Motors per Birkhoff,[5] Garabedian, i Carl R. de Boor,[6] tots pels treballs fets al començament de la dècada del 1960 o finals de la del 1950. Pel capbaix un dels articles de de Casteljau es va publicar, però no es va difondre àmpliament, el 1959. El treball de De Boor a General Motors va resultar en un cert nombre d'articles que es varen publicar durant els primers anys de la dècada del 1960, incloent-hi part del treball fonamental en B-splines.[7]

També s'hi estava treballant a Pratt & Whitney Aircraft, on treballaven dos dels autors de Ahlberg et al.[8] el primer tractat dels splines de l'extensió d'un llibre -, i la David Taylor Model Basin de Feodor Theilheimer. El treball a General Motors es detalla de manera esplèndida a Notices of the AMS de Birkhoff i Young.[9] Davis resumí part d'aquest material a SIAM News.[7]

Vegeu també

Referències

  1. ↑ Epperson, History of Splines, Na Digest, volums 98, núm. 26, 1998.
  2. ↑ Schoenberg, Contributions to the problem of approximation of equidistant data by analytic functions, Quart. Appl. Math., volums 4, pàg. 45-99 i 112-141, 1946.
  3. ↑ Bartels, Beatty, and Barsky, An Introduction to Splines for Use in Computer Graphics and Geometric Modeling, 1987.
  4. ↑ Ferguson, James C, Multi-variable curve interpolation, J. ACM, volums 11, núm. 2, pàg. 221-228, abr. de 1964.
  5. ↑ Birkhoff, Fluid dynamics, reactor computations, and surface representation, a: Steve Nash (ed.), A History of Scientific Computation, 1990.
  6. ↑ Birkhoff i de Boor, Piecewise polynomial interpolation and approximation, en: H. L. Garabedian (ed.), Proc. Simposi de General Motors de 1964, pàg. 164-190. Elsevier, Nova York i Amsterdam, 1965
  7. ↑ 7,0 7,1 Davis, B-splines and Geometric design, SIAM News, vol. 29, no. 5, 1997.
  8. ↑ Ahlberg, Nilson, and Walsh, The Theory of Splines and Their Applications, 1967.
  9. ↑ Young, Garrett Birkhoff and applied mathematics, Notices of the AMS, vol. 44, no. 11, pp. 1446–1449, 1997.

Bibliografia addicional

  • Stoer; Bulirsch. Introduction to Numerical Analysis. Springer Science+Business Media, p. 93–106. ISBN 0387904204. 
  • Chapra, Canale. Numerical Methods for Engineers. 5a ed.. 

Enllaços externs

  • Spline Corbes, el prof. henri de Donald Casa Clemson University
  • An Interactive Introduction to Splines, ibiblio.org
  • Introduction to Splines, codeplea.com
  • Utilitat d'interpolació d'splines cúbics en línia
  • Learning by Simulations Simulació interactiva de diversos cúbics.
  • Simètric Spline Corbes, una animació de Theodore Gray, a The Wolfram Demonstrations Project DE WOLFRAMI, 2007.