Serie di Fourier

In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier.

Storia

La serie prende il nome dal matematico francese Joseph Fourier (1768-1830), il quale fu il primo a studiare sistematicamente tali serie infinite. In precedenza esse erano state oggetto di investigazioni preliminari da parte di Eulero, d'Alembert e Daniel Bernoulli. Fourier applicò tali serie alla soluzione dell'equazione del calore, pubblicando i suoi risultati iniziali nel 1807 e nel 1811. L'opera più ampia, intitolata Théorie analytique de la chaleur, fu pubblicata nel 1822. Dopo la metà del secolo Dirichlet e Riemann riformularono i risultati di Fourier con maggiore rigore e precisione e in forma più soddisfacente.

Successivamente sono state introdotte molte altre forme di trasformate integrali che hanno esteso l'idea iniziale di rappresentare ogni funzione periodica come sovrapposizione di armoniche. Esistono infatti molte altre successioni di funzioni ortogonali che godono di proprietà simili a quelle dell'analisi di Fourier, spesso corrispondenti a soluzioni di una opportuna equazione differenziale come, ad esempio, le successioni di funzioni di Bessel. Un'ampia classe di successioni utili, inoltre, è quella delle soluzioni dei cosiddetti problemi di Sturm-Liouville. Essi si riconducono anche alle soluzioni di equazioni di Schrödinger della meccanica ondulatoria.

Definizione

Un polinomio trigonometrico è una funzione periodica di periodo ${\displaystyle 2\pi }$ definita sul campo reale del tipo^[1]

${\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\left[a_{n}\cos(nt)+b_{n}\sin(nt)\right],}$

${\displaystyle f(t)=\sum _{n=-N}^{N}c_{n}e^{int},}$

dove i coefficienti ${\displaystyle a_{n}}$ e ${\displaystyle b_{n}}$ sono numeri reali, i coefficienti ${\displaystyle c_{n}}$ sono in generale complessi ed ${\displaystyle n}$ è intero. La seconda forma si ricava dalla prima applicando la formula di Eulero.

Si definiscano, al variare di ${\displaystyle n\in \mathbb {Z} }$, le funzioni

${\displaystyle u_{n}(t)=e^{int},}$

e sia

${\displaystyle \langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t){\overline {g(t)}}\,\mathrm {d} t}$

un prodotto interno in ${\displaystyle L^{2}(T)}$, dove ${\displaystyle T}$ è l'intervallo ${\displaystyle [-\pi ,\pi ]}$.

Allora ${\displaystyle \{u_{n}=e^{int},n\in \mathbb {Z} \}}$ è un sistema di funzioni ortonormali rispetto al prodotto interno così definito. Si ha infatti^[2]

${\displaystyle \langle u_{n},u_{m}\rangle ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{i(n-m)t}\,\mathrm {d} t=\delta _{n,m}.}$

Un tale sistema ortonormale in ${\displaystyle L^{2}(T)}$ è detto sistema ortonormale trigonometrico, ed è un sistema completo.

Si definisce serie di Fourier di una funzione ${\displaystyle f\in L^{2}(T)}$ a quadrato sommabile la rappresentazione della funzione per mezzo di una combinazione lineare dei vettori di base ${\displaystyle u_{n}}$ del sistema ortonormale trigonometrico:^[3]

${\displaystyle \sum _{n=-\infty }^{\infty }f_{n}u_{n}=\sum _{n=-\infty }^{\infty }f_{n}e^{int}.}$

I coefficienti della combinazione sono quindi la proiezione della funzione sui vettori di base stessi

${\displaystyle f_{n}={\frac {\langle f,u_{n}\rangle }{\|u_{n}\|^{2}}}=\langle f,u_{n}\rangle ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)e^{-int}\,\mathrm {d} t}$

e sono detti coefficienti di Fourier.

Le somme parziali della serie di Fourier sono ottenute troncando la serie in modo simmetrico

${\displaystyle S_{N}(t)=\sum _{n=-N}^{N}f_{n}e^{int},\qquad N=0,1,2\dots .}$

La serie di Fourier di una funzione può essere espressa in diverse forme matematicamente equivalenti: rettangolare, complessa e polare.

Forma rettangolare

Si consideri una funzione di una variabile reale a valori complessi ${\displaystyle \,f(x)}$ che sia periodica con periodo ${\displaystyle 2\pi }$ e a quadrato integrabile sull'intervallo ${\displaystyle \,[0,2\pi ]}$. Si definiscono i coefficienti tramite la formula di analisi:

${\displaystyle F_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)e^{-inx}\,\mathrm {d} x}$

e la rappresentazione mediante serie di Fourier di ${\displaystyle f(x)}$ è allora data dalla formula di sintesi

${\displaystyle f(x)=\sum _{n=-\infty }^{\infty }F_{n}\,e^{inx}.}$

Ciascuno dei termini di questa somma è chiamato modo di Fourier. Nell'importante caso particolare nel quale la ${\displaystyle f(x)}$ è una funzione a valori reali, spesso risulta utile servirsi dell'identità ${\displaystyle e^{inx}=\cos(nx)+i\sin(nx)}$ per rappresentare equivalentemente ${\displaystyle \,f(x)}$ come combinazione lineare infinita di funzioni della forma ${\displaystyle \cos(nx)}$ e ${\displaystyle \sin(nx)}$. Si ottiene la serie di Fourier:

${\displaystyle f(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left({\frac {2\pi }{T}}nx\right)+b_{n}\sin \left({\frac {2\pi }{T}}nx\right)\right].}$

Con ${\displaystyle T}$ periodo della funzione e dove:

${\displaystyle {\begin{aligned}a_{0}&={\frac {2}{T}}\int _{-T/2}^{T/2}f(x)\,\mathrm {d} x,\\a_{n}&={\frac {2}{T}}\int _{-T/2}^{T/2}f(x)\cos \left({\frac {2\pi }{T}}nx\right)\,\mathrm {d} x,\\b_{n}&={\frac {2}{T}}\int _{-T/2}^{T/2}f(x)\sin \left({\frac {2\pi }{T}}nx\right)\,\mathrm {d} x.\end{aligned}}}$

Per funzioni pari compaiono solo i coseni:

${\displaystyle {\begin{aligned}a_{0}&={\frac {4}{T}}\int _{0}^{T/2}f(x)\,\mathrm {d} x,\\a_{n}&={\frac {4}{T}}\int _{0}^{T/2}f(x)\cos \left({\frac {2\pi }{T}}nx\right)\,\mathrm {d} x,\\b_{n}&=0,\end{aligned}}}$

mentre per funzioni dispari compaiono solo i seni:

${\displaystyle {\begin{aligned}a_{0}&=a_{n}=0,\\b_{n}&={\frac {4}{T}}\int _{0}^{T/2}f(x)\sin \left({\frac {2\pi }{T}}nx\right)\,\mathrm {d} x.\end{aligned}}}$

I coefficienti ${\displaystyle a_{n}}$ e ${\displaystyle b_{n}}$ esprimono le ampiezze, ovvero i pesi delle sinusoidi e cosinusoidi, e ${\displaystyle a_{0}/2}$ corrisponde al valore medio in un periodo della funzione ${\displaystyle f(x)}$. Tale formulazione si riconduce alla precedente rappresentazione se:

${\displaystyle F_{n}={\frac {a_{n}-ib_{n}}{2}},}$

e

${\displaystyle F_{n}=F_{-n}^{*}.}$

Forma complessa

La serie di Fourier in forma complessa di una funzione ${\displaystyle f(x)}$ è:

${\displaystyle f(x)=\sum _{n=-\infty }^{\infty }\gamma _{n}e^{\frac {i2\pi nx}{T}},}$

in cui ${\displaystyle \gamma _{n}\in \mathbb {C} }$ e ${\displaystyle i^{2}=-1.}$

I coefficienti ${\displaystyle \gamma _{n}}$ sono calcolati tramite la relazione:

${\displaystyle \gamma _{n}={\frac {1}{T}}\int _{0}^{T}f(x)e^{\frac {-i2\pi nx}{T}}dx.}$

Se la funzione ${\displaystyle f(x)}$ è reale i coefficienti ${\displaystyle \gamma _{n}}$ soddisfano la proprietà di simmetria hermitiana:

${\displaystyle \gamma _{n}^{*}=\gamma _{-n}.}$

Questo fatto si può vedere esplicitando la somma dei termini di ordine ${\displaystyle n}$ e ${\displaystyle -n}$ della serie:

${\displaystyle \gamma _{n}e^{inx}+\gamma _{-n}e^{-inx}=\gamma _{n}[\cos(nx)+i\sin(nx)]+\gamma _{-n}[\cos(-nx)+i\sin(-nx)].}$

Da cui, servendosi delle proprietà delle funzioni trigonometriche (in particolare della parità del coseno e della disparità del seno) si trova:

${\displaystyle \gamma _{n}e^{inx}+\gamma _{-n}e^{-inx}=(\gamma _{n}+\gamma _{-n})\cos(nx)+(\gamma _{n}-\gamma _{-n})i\sin(nx).}$

Si vede dunque che per avere una funzione reale descritta in serie di Fourier, la quantità ${\displaystyle \gamma _{n}+\gamma _{-n}}$ deve essere reale, mentre la quantità ${\displaystyle \gamma _{n}-\gamma _{-n}}$ deve essere immaginaria pura per ogni ${\displaystyle n\in \mathbb {Z} }$. Entrambe le condizioni sono verificate dalla proprietà di simmetria hermitiana dei coefficienti.

Forma polare

Un'altra forma in cui è possibile esprimere la serie di Fourier di una funzione ${\displaystyle f(x)}$ reale è la forma polare:

${\displaystyle f(x)=c_{0}+2\sum _{n=1}^{\infty }c_{n}\cos \left({\frac {2\pi nx}{T}}+\phi _{n}\right).}$

I coefficienti ${\displaystyle c_{0}}$, ${\displaystyle c_{n}}$ e ${\displaystyle \phi _{n}}$ possono essere definiti partendo dai coefficienti ${\displaystyle \gamma _{n}}$ della forma complessa:

${\displaystyle c_{0}=\gamma _{0},\quad \quad c_{n}=|\gamma _{n}|,\quad \quad \phi _{n}=\angle \gamma _{n}.}$

Convergenza delle serie di Fourier

In generale, la serie di Fourier di una funzione continua definita sulla circonferenza unitaria non converge alla funzione stessa, e di conseguenza la scrittura:

${\displaystyle f(x)=\lim _{n\rightarrow \infty }S_{n}(f,x)=\lim _{n\rightarrow \infty }{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(t)\sum _{k=-n}^{n}e^{ikt}\mathrm {d} t}$

non vale per ogni funzione.^[4] Questo può essere provato, ad esempio, attraverso il teorema di Banach-Steinhaus. In particolare, per ogni numero reale ${\displaystyle x}$ esiste un sottoinsieme denso ${\displaystyle E_{x}}$ dello spazio ${\displaystyle C(T)}$ delle funzioni continue definite su ${\displaystyle T}$ tale che:^[5]

${\displaystyle \sup _{n}|S_{N}(f,x)|=\infty ,\quad \forall f\in E_{x}.}$

Si dimostra tuttavia che per ${\displaystyle f\in C(T)}$ esiste un polinomio trigonometrico ${\displaystyle P}$ tale che:

${\displaystyle |f(t)-P(t)|<\epsilon ,}$

per ogni ${\displaystyle t}$ reale. In particolare, nel 1904 il matematico ungherese Lipót Fejér mostrò che la media aritmetica delle somme parziali della serie di Fourier di ${\displaystyle f}$ converge uniformemente al valore della funzione stessa.^[3]

Nonostante i coefficienti di Fourier ${\displaystyle \,a_{n}}$ e ${\displaystyle \,b_{n}}$ si possano definire formalmente per ogni funzione tale per cui abbia senso considerare gli integrali che li caratterizzano, la convergenza della serie definita attraverso di essi alla funzione dipende dalle proprietà specifiche di tale funzione. Se ${\displaystyle \,f(x)}$ è a quadrato integrabile si ha:

${\displaystyle \lim _{N\rightarrow \infty }\int _{-\pi }^{\pi }\left|f(x)-\sum _{n=-N}^{N}F_{n}\,e^{inx}\right|^{2}\,dx=0,}$

ottenendo così una convergenza nella norma dello spazio L².

Esistono altri criteri che consentono di garantire che la serie converga in un dato punto, ad esempio il fatto che la funzione sia differenziabile nel punto. Anche una discontinuità con salto è accettabile, poiché se la funzione possiede derivate a sinistra e a destra allora la serie di Fourier converge al valore medio dei rispettivi limiti a sinistra e a destra. Si può tuttavia riscontrare il fenomeno di Gibbs, e si ha la possibilità che la serie di Fourier di una funzione continua non converga punto per punto.

Proprietà

Le proprietà delle serie di Fourier sono in gran parte conseguenze delle proprietà di ortogonalità e di omomorfismo delle funzioni ${\displaystyle e^{inx}}$, ed in generale delle proprietà del gruppo delle rotazioni. Le funzioni ${\displaystyle e^{ikx}}$ appartenenti alla base ortonormale sono omomorfismi del gruppo additivo della retta reale sul gruppo circolare, ovvero dell'insieme dei numeri complessi di modulo unitario dotato dell'ordinaria moltiplicazione del campo complesso. Come conseguenza di questo fatto, se:

${\displaystyle g(x)=f(x-y),}$

allora, denotando con ${\displaystyle G}$ la trasformata di ${\displaystyle g}$, si ha:

${\displaystyle G_{k}=e^{-iky}F_{k}.}$

Inoltre, se ${\displaystyle H_{k}}$ è la trasformata di ${\displaystyle h=f*g}$, allora:

${\displaystyle H_{k}=F_{k}G_{k}.}$

Ossia, il coefficiente di Fourier della convoluzione di due funzioni è il prodotto dei coefficienti di Fourier dello stesso grado delle due funzioni stesse.

Scambiando i ruoli di prodotto usuale e prodotto di convoluzione, se ${\displaystyle h=f\cdot g}$ allora i coefficienti di tale funzione prodotto sono dati dalla convoluzione su ${\displaystyle \mathbb {Z} }$ dei coefficienti delle funzioni ${\displaystyle f}$ e ${\displaystyle g}$:

${\displaystyle H_{k}=\sum _{i=-\infty }^{\infty }F_{i}\,G_{k-i}.}$

I teoremi di Riesz-Fischer e Parseval determinano inoltre due importanti proprietà delle serie di Fourier.

Il teorema di Riesz-Fischer

Il teorema di Riesz-Fischer stabilisce che in uno spazio completo ogni successione in ${\displaystyle \ell ^{2}}$ definisce una funzione a quadrato integrabile. In particolare, il teorema determina le condizioni per cui gli elementi di una successione in ${\displaystyle \ell ^{2}}$ sono i coefficienti di Fourier di un qualche vettore di ${\displaystyle L^{2}}$.

Sia ${\displaystyle \{u_{n}\}}$ un sistema ortonormale di polinomi in uno spazio di Hilbert ${\displaystyle H}$ e sia ${\displaystyle c_{n}}$ una successione. Allora esiste un unico vettore ${\displaystyle f\in H}$ tale che gli elementi della successione siano i coefficienti di Fourier di ${\displaystyle f:}$^[6]

${\displaystyle c_{n}=(f,u_{n}),}$

dove ${\displaystyle (\cdot ,\cdot )}$ è un prodotto interno. La successione definisce quindi una funzione ${\displaystyle f}$ in ${\displaystyle L^{2}}$.

Il teorema di Parseval

Siano ${\displaystyle A(x)}$ e ${\displaystyle B(x)}$ due funzioni Riemann integrabili a valori complessi definite su ${\displaystyle \mathbb {R} }$. Siano esse periodiche con periodo ${\displaystyle 2\pi }$; e siano le loro serie di Fourier date rispettivamente da:

${\displaystyle A(x)=\sum _{n=-\infty }^{\infty }a_{n}e^{inx},\qquad B(x)=\sum _{n=-\infty }^{\infty }b_{n}e^{inx}.}$

Allora:^[7]

${\displaystyle \sum _{n=-\infty }^{\infty }a_{n}{\overline {b_{n}}}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }A(x){\overline {B(x)}}dx.}$

Come caso particolare, se ${\displaystyle A(x)=B(x)=f(x)\in L^{2}([-\pi ,\pi ]),}$ si ha:

${\displaystyle \sum _{n=-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}\,dx.}$

Esempio

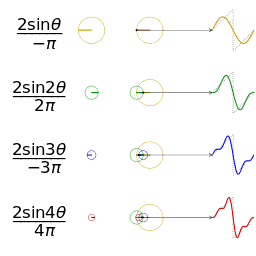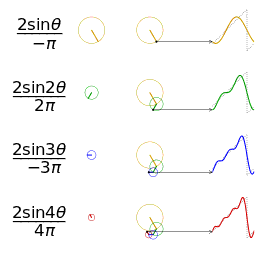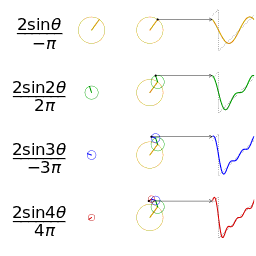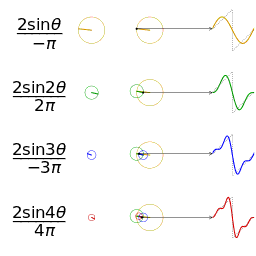
Si consideri la funzione ${\displaystyle f(x)=x}$ (funzione identità) per ${\displaystyle x\in [-\pi ,\pi ]}$. Se si vuole considerare il suo sviluppo all'esterno di questo dominio, la serie di Fourier richiede implicitamente che questa funzione sia periodica (l'estensione periodica della funzione identità è una funzione a dente di sega).

Per calcolare i coefficienti di Fourier di questa funzione conviene osservare che ${\displaystyle f}$ è una funzione dispari, quindi si esprimerà come una somma solo di seni, dato che ${\displaystyle \sin(nx)}$è una funzione dispari. Osservare la parità della funzione aiuta a ridurre i calcoli perché annulla dei coefficienti (in questo caso quelli del coseno).

${\displaystyle {\frac {a_{0}}{2}}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)\,\mathrm {d} x={\frac {1}{2\pi }}\int _{-\pi }^{\pi }x\,\mathrm {d} x=0,}$

${\displaystyle a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)\,\mathrm {d} x={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos(nx)\,\mathrm {d} x=0,}$

${\displaystyle {\begin{aligned}b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)\,\mathrm {d} x={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin(nx)\,\mathrm {d} x\\&={\frac {2}{\pi }}\int _{0}^{\pi }x\sin(nx)\,\mathrm {d} x={\frac {2}{\pi }}\left(\left[-{\frac {x\cos(nx)}{n}}\right]_{0}^{\pi }+\left[{\frac {\sin(nx)}{n^{2}}}\right]_{0}^{\pi }\right)=(-1)^{n+1}{\frac {2}{n}}.\end{aligned}}}$

Quindi la serie di Fourier per la funzione in esame è:

${\displaystyle f(x)=x={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}\cos(nx)+b_{n}\sin(nx))=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {2}{n}}\sin(nx),\qquad \forall x\in (-\pi ,\pi ).}$

Può essere interessante vedere l'applicazione della serie di Fourier al calcolo del valore ${\displaystyle \zeta (2)}$ della funzione zeta di Riemann.

Note

Bibliografia

• (EN) Walter Rudin, Real and Complex Analysis, Mladinska Knjiga, McGraw-Hill, 1970, ISBN 0-07-054234-1.
• Carlo Cercignani, Teoria e applicazioni della serie di Fourier, Milano, Tamburini Editore, 1972.
• Ulisse Dini (1880): Serie di Fourier e altre rappresentazioni analitiche delle funzioni di una variabile reale T. Nistri.
• (EN) William E. Byerly (1893): An elementary treatise on Fourier's series and spherical, cylindrical, and ellipsoidal harmonics with applications to problems in mathematical physics Ginn & Company.
• (EN) Horatio S. Carslaw (1921): Introduction to the theory of Fourier's series and integrals, Macmillan & co., ltd.
• (EN) E. W. Hobson (1926): The Theory Of Functions Of A Real Variable And The Theory Of Fourier's Series Vol. 2, Cambridge University Press.
• (EN) Antoni Zygmund (1935): Trigonometrical series, Subwencji Fundusz Kultury Narodowej
• (EN) Yitzhak Katznelson (1976): An introduction to harmonic analysis, Second corrected edition. Dover Publications, ISBN 0-486-63331-4

Voci correlate

• Analisi armonica
• Analisi di Fourier
• Base (algebra lineare)
• Calcolo umbrale
• Convoluzione
• Fenomeno di Gibbs
• Polinomio trigonometrico
• Rappresentazione spettrale dei segnali
• Spazio di Hilbert
• Teorema di Parseval
• Teorema di Riesz-Fischer
• Teoria di Sturm-Liouville
• Trasformata di Fourier

Altri progetti

• Wikizionario contiene il lemma di dizionario «serie di Fourier»
• Wikimedia Commons contiene immagini o altri file sulla serie di Fourier

Collegamenti esterni

• (EN) Fourier series, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Serie di Fourier, su MathWorld, Wolfram Research.
• (EN) Serie di Fourier, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• Java applet che visualizza lo sviluppo in serie di Fourier di una qualsiasi funzione

V · D · M Successioni e Serie
Successioni di interi	Base Progressione aritmetica · Progressione geometrica · Progressione armonica · Progressione aritmetica · Numeri quadrati · Numeri cubici · Fattoriale · Potenze di 2 · Potenze di 3 · Potenze di 10 Avanzate Successione completa · Numeri di Fibonacci · Numeri figurati · Numeri ettagonali · Numeri esagonali · Numeri di Lucas · Numeri di Pell · Numeri pentagonali · Numero poligonale · Numero triangolare
Proprietà delle successioni	Successione di Cauchy · Successione monotona · Successione alternata
Proprietà delle serie	Tendenza Serie alternata · Serie convergente · Serie divergente · Serie telescopica Convergenza Convergenza incondizionata · Convergenza assoluta · Convergenza uniforme
Serie esplicite	Convergenti 1/2 − 1/4 + 1/8 − 1/16 + ⋯ · 1/2 + 1/4 + 1/8 + 1/16 + ⋯ · 1/4 + 1/16 + 1/64 + 1/256 + ⋯ · 1 + 1/2s+ 1/3s + ... (Riemann zeta) Divergenti 1 + 1 + 1 + 1 + ⋯ · 1 + 2 + 3 + 4 + ⋯ · 1 + 2 + 4 + 8 + ⋯ · 1 − 1 + 1 − 1 + ⋯ (Grandi) · a1 + (a1+d) + ⋯ · 1 − 2 + 3 − 4 + ⋯ · 1 − 2 + 4 − 8 + ⋯ · 1 + 1/2 + 1/3 + 1/4 + ⋯ (armonica) · 1 − 1 + 2 − 6 + 24 − 120 + ⋯ (fattoriale alternata) · 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ⋯ (inversi dei primi)
Tipi di serie	Serie di Taylor · Serie di potenze · Serie formale di potenze · Serie di Laurent · Serie di Puiseux · Serie di Dirichlet · Serie trigonometrica · Serie di Fourier · Serie generatrice
Serie Ipergeometrica	Serie ipergeometrica generalizzata · Funzione ipergeometrica di un argomento di matrice · Serie di Lauricella · Serie modulare · Serie ipergeometrica confluente · Serie theta

Controllo di autorità	Thesaurus BNCF 35891 · LCCN (EN) sh85051090 · GND (DE) 4155109-6 · BNE (ES) XX540313 (data) · BNF (FR) cb11979488t (data) · J9U (EN, HE) 987007548250805171 · NDL (EN, JA) 00562088