Distribució binomial

Distribució binomial

Funció de distribució de probabilitat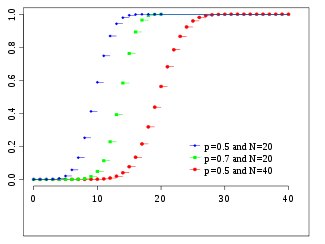
Tipus	Distribució binomial de Poisson, Panjer distribution (en) , Distribució multinomial, distribució univariant i distribució de probabilitat discreta
Paràmetres	${\displaystyle n\geq 0}$ nombre d'assaigs (sencer) ${\displaystyle 0\leq p\leq 1}$ probabilitat d'èxit (real)
Suport	${\displaystyle k\in \{0,\dots ,n\}\!}$
FD	${\displaystyle I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )\!}$
Esperança matemàtica	${\displaystyle np\!}$
Mediana	${\displaystyle \lfloor np\rfloor }$ o ${\displaystyle \lceil np\rceil }$[1]
Moda	${\displaystyle \lfloor (n+1)\,p\rfloor \!}$ o ${\displaystyle \lceil (n+1)\,p\rceil -1\!}$
Variància	${\displaystyle np(1-p)\!}$
Coeficient de simetria	${\displaystyle {\frac {1-2p}{\sqrt {np(1-p)}}}\!}$
Curtosi	${\displaystyle {\frac {1-6p(1-p)}{np(1-p)}}\!}$
Entropia	${\displaystyle {\frac {1}{2}}\ln \left(2\pi Nep(1-p)\right)+O\left({\frac {1}{n}}\right)}$
FGM	${\displaystyle \left(p\left(\mathrm {e} ^{t}-1\right)+1\right)^{n}}$
FC	${\displaystyle (1-p+pe^{it})^{n}\!}$
Mathworld	BinomialDistribution

En Teoria de la probabilitat i en estadística, una variable aleatòria ${\displaystyle X}$ es diu que té una distribució binomial de paràmetres ${\displaystyle n}$ i ${\displaystyle p}$ si representa el nombre d'èxits en ${\displaystyle n}$ repeticions independents d'una prova que té probabilitat d'èxit ${\displaystyle p}$. Per exemple, tirem 10 vegades un dau ordinari i comptem quantes vegades surt un 6; en aquest cas l'èxit és "treure un 6", i la variable que compta el nombre de sisos té una distribució binomial de paràmetres ${\displaystyle n=10}$ i ${\displaystyle p=1/6}$.

La distribució binomial és la base de la popular prova binomial de significació estadística.^[2]

Va ser proposada pel matemàtic i físic suís Jacob Bernoulli.^[3]

Distribució de Bernoulli

Les distribucions binomials s'inscriuen en el marc de referència de les distribucions de Bernoulli. S'anomena experiència de Bernoulli aquell experiment aleatori del qual només s'estudia la verificació o no d'un esdeveniment ${\displaystyle A}$ que pot donar-se amb probabilitat ${\displaystyle P(A)=p.}$ La realització de l'esdeveniment ${\displaystyle A}$ s'anomena èxit. S'acostuma a representar la probabilitat del complementari (no ${\displaystyle A}$), la realització del qual s'anomena fracàs, per ${\displaystyle P({\text{no}}\ A)=q;}$ és clar que ${\displaystyle p+q=1.}$

Així, un experiment o experiència de Bernoulli es caracteritza per ser dicotòmic, és a dir, només són possibles dos resultats: èxit o fracàs.

Exemples d'experiències de Bernoulli

1. Es llança una moneda, l'esdeveniment A podria ser "que surti cara".
2. En una bossa hi ha boles blanques, negres i vermelles. traiem una bola i mirem si és de color blanc o no. L'esdeveniment A podria ser "treure bola blanca".
3. En un referèndum amb possibles respostes Sí o No, l'esdeveniment A podria ser "que surti Sí".

Distribució binomial

La distribució binomial és una distribució de probabilitat discreta que fa el recompte del nombre de vegades que es verifica l'èxit (realització de l'esdeveniment ${\displaystyle A}$) quan es repeteix ${\displaystyle n}$ vegades, de forma independent i en les mateixes condicions, una experiència de Bernouilli.

Per n = 1, la distribució binomial és una distribució de Bernoulli.

Designem per X la variable aleatòria que mesura el nombre d'èxits que s'han produït en els n experiments. Per indicar que segueix una distribució binomial de paràmetres n i p , s'escriu:

$${\displaystyle X\sim B(n,p)\,}$$

Exemples

Les següents situacions són exemples d'experiments que poden modelitzar per aquesta distribució:

• Es llança un dau deu vegades i es compta el nombre de sisos obtinguts: X ~ B(10, 1/6)
• Es llança una moneda dues vegades i es compta el nombre de cares obtingudes, tenim ${\displaystyle B(2,0'5).}$
• Una partícula es mou unidimensionalment amb probabilitat ${\displaystyle q}$ de moure's una unitat de distància cap enrere i ${\displaystyle p=1-q}$ de moure's una unitat cap endavant. Després de ${\displaystyle n}$ moviments, el nombre de vegades que s'ha mogut cap endavant és una variable binomial ${\displaystyle B(n,p)}$ .

Propietats característiques

Mitjana i Variància

Sigui ${\displaystyle X\sim B(n,p)\,}$ una variable aleatòria binomial de paràmetres ${\displaystyle n}$ i ${\displaystyle p}$.

$${\displaystyle \mathbb {E} [X]=np\,}$$

Això es dedueix per la linealitat de l'esperança, ja que X és la suma de n variables aleatòries de Bernoulli idèntiques, cadascuna d'elles amb esperança p. És a dir, si ${\displaystyle X_{1},\ldots ,X_{n}}$ són variables aleatòries iguals (i independents) de Bernoulli amb paràmetre p, aleshores

i, atès que tindrem que D'altra banda, per a una variable de Bernoulli, d'on Llavors, de la independència de ${\displaystyle X_{1},\dots ,X_{n}}$, es dedueix que

$${\displaystyle {\text{Var}}[X]=np(1-p).}$$

Funció de probabilitat

Sigui ${\displaystyle X}$ una variable aleatòria binomial de paràmetres ${\displaystyle n}$ i ${\displaystyle p}$. Aleshores la probabilitat d'obtenir exactament ${\displaystyle k\,\!}$ èxits en ${\displaystyle n\,\!}$ repeticions (proves) independents de Bernouilli és:

on és el coeficient binomial.

Així, la funció de probabilitat de ${\displaystyle X}$ és

Funció de distribució

$${\displaystyle F(x)=\Pr(X\leq x)={\begin{cases}0,&{\text{si}}\,x<0,\\\displaystyle {\sum _{i=0}^{\lfloor x\rfloor }{n \choose i}p^{i}(1-p)^{n-i}},&{\text{si}}\,x\in [0,n],\\1,&{\text{si}}\,x>n.\end{cases}}}$$

on ${\displaystyle [x]}$ denota la part entera de ${\displaystyle x}$.

Exemple

Suposem que tenim una moneda trucada amb probabilitat 0.3 que surti cara. La probabilitat que surtin 4 cares en 6 llançaments és

$${\displaystyle f(4)={\binom {6}{4}}0.3^{4}(1-0.3)^{6-4}=0.059535.}$$

Aproximació de la distribució binomial per les distribucions de Poisson i normal

Si ${\displaystyle n}$ tendeix a infinit i ${\displaystyle p_{n}\,\!}$ és tal que ${\displaystyle \lim _{n\to \infty }n\,p_{n}=\lambda }$, llavors la distribució d'una variable aleatòria binomial de paràmetres ${\displaystyle n}$ i ${\displaystyle p_{n}}$tendeix a una distribució de Poisson de paràmetre ${\displaystyle \lambda }$.

D'altra banda, pel teorema central del límit, quan n és gran (normalment s'exigeix que ${\displaystyle n\geq 30}$) la distribució binomial es pot aproximar mitjançant la distribució normal.

Propietats reproductives

Donades m variables binomials independents ${\displaystyle X_{i}}$, i = 1, ..., m, de paràmetres ${\displaystyle n_{i}}$ i ${\displaystyle p_{i}}$, respectivament, la seva suma S és també una variable binomial, de paràmetres ${\displaystyle n_{1}+\cdots +n_{m}}$ i ${\displaystyle p}$, és a dir,

$${\displaystyle S=\sum _{i=1}^{m}X_{i}\sim B\left(\sum _{i=1}^{m}n_{i},p\right).}$$

Referències

Vegeu també

• Distribució hipergeomètrica
• Distribució multinomial