Nombre racional

S'anomena nombre racional a tot aquell nombre que pot ser expressat com a resultat de la divisió de dos nombres enters, amb el divisor diferent de 0. El conjunt dels racionals es representa amb la lletra ℚ (${\displaystyle \mathbb {Q} }$) o Q, de quocient. Aquest conjunt de nombres conté el dels nombres enters i és un subconjunt dels nombres reals.^[1] Els reals que no pertanyen a aquest conjunt s'anomenen irracionals.

Els racionals es caracteritzen per tenir un desenvolupament decimal (o en qualsevol base) finit o periòdic, és a dir que un racional té un nombre de xifres decimals finit, o bé que aquestes es repeteixen de manera regular.^[2][3]

Història

És versemblant que el concepte de nombre fraccionari dati dels temps prehistòrics. Fins i tot els antics egipcis van escriure textos matemàtics que descrivien com convertir fraccions generals en les seves fraccions amb notació especial. Els matemàtics indis i de la Grècia clàssica van fer estudis sobre la teoria dels nombres racionals, com a part de l'estudi general de la teoria de nombres. El més conegut de tots és l'anomenat Elements d'Euclides, que data aproximadament del 300 aC. Dels textos indis el més rellevant és el Sthananga Sutra, el qual també tracta sobre la teoria dels nombres com a part d'un estudi general de matemàtiques.

El concepte de fracció decimal està lligat estretament a la notació amb valor posicional decimal; tots dos sembla que s'hagin desenvolupat en paral·lel. Per exemple, és habitual en les matemàtiques de Sutra incloure càlculs d'aproximacions en fraccions decimals de pi o de l'arrel quadrada de dos. De manera similar, els textos matemàtics babilonis havien fet servir sempre fraccions sexagesimals freqüentment.

Definició

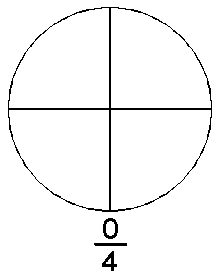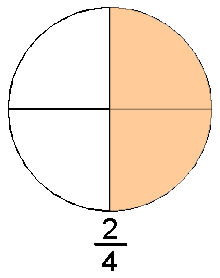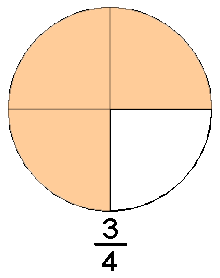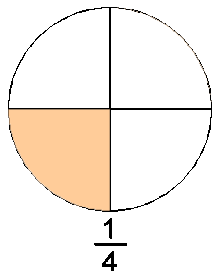
La forma intuïtiva d'entendre els nombres racionals és pensar en ells com els nombres que resulten de les fraccions. Una fracció es compon de dos nombres enters, un numerador n i un denominador d. La fracció es pot entendre com la quantitat d'una cosa que es mesura en unitats que es poden dividir. La unitat d'aquesta cosa es parteix en un nombre d de parts iguals i se'n agafen n d'aquestes parts. A la figura de l'esquerra es parteix un cercle (que es pot fer servir com unitat de mesura de la matèria de què està fet) en quatre parts iguals, agafant-ne una, dues, tres, o quatre d'aquestes parts s'obtenen diferents quantitats de la matèria de la qual està fet el cercle. Si s'agafen menys de 4 parts es té menys d'una unitat de matèria, si se'n agafen més de 4 s'obtindria més d'una unitat, si se'n agafen exactament quatre es tindria una unitat.

Una manera de definir els nombres naturals sense necessitat de fer referència a objectes físics que es parteixen en parts iguals, seria definir-los com parelles de nombres enters. El que passa és que aquesta definició no seria completament satisfactòria doncs no coincidiria exactament amb el concepte intuïtiu que s'ha explicat abans.

Fixeu-vos que si el mateix cercle es parteix en vuit parts i se'n agafen quatre es té la mateixa quantitat de matèria que si es parteix en quatre parts i se'n agafen dues. Però la parella (4,8) no és la mateixa parella de nombres que la parella (2,4). Per poder definir els nombres racionals com a parelles de nombres enters cal fer quelcom per identificar la parella (4,8) amb la (2,4) i assignar-los a totes dues (i a d'altres que corresponen a la mateixa quantitat de matèria) el mateix nombre racional abstracte.

Un altre problema que cal superar amb la idea de les parelles és que un objecte no es pot partir en zero parts, per tant parelles com la (3,0) s'han de prohibir.

Tenint en compte tot això el conjunt dels nombres racionals es defineix com:

El conjunt de les classes d'equivalència de parelles ordenades d'enters ${\displaystyle \left(a,b\right)}$, amb ${\displaystyle b}$ diferent de zero, amb la següent relació d'equivalència:

${\displaystyle \left(a,b\right)\sim \left(c,d\right){\mbox{ si i només si }}ad=bc.}$

Aquesta relació d'equivalència en el cas de l'exemple funciona bé (2x8=4x4) és a dir fa que les dues parelles de nombres enters pertanyin a la mateixa classe d'equivalència, per tant la definició els assigna el mateix nombre racional.

La forma de veure que això funcionarà sempre tal com intuïtivament es desitja és observar que si dues quantitats de matèria són iguals, al multiplicar-les per un mateix nombre enter continuaran sent iguals. La idea és veure que passa si es multipliquen dues fraccions per un nombre enter que és el producte dels dos denominadors.

Per començar la idea de multiplicar s'ha d'extrapolar de la idea de multiplicar nombres naturals. Intuïtivament, multiplicar un nombre racional per un nombre natural m ha de coincidir amb sumar el nombre racional amb si mateix m vegades. Però si el significat de (n,d) és que s'han agafat n bocins iguals, agafar n bocins m vegades serà igual a agafar m x n bocins i per tant ${\displaystyle m\!\times \!(n,d)=(m\!\times \!n,d)}$.

Tot seguit s'ha de veure que cada d bocins es té una unitat per tant cal identificar el nombre racional (dxa,d) amb el nombre natural a.

Ara ja es pot comprovar que la relació d'equivalència definida porta on intuïtivament es desitja:

${\displaystyle {\begin{aligned}&b\times d\times \left(a,b\right)=\left(b\times d\times a,b\right)=d\times a\\&b\times d\times \left(c,d\right)=\left(b\times d\times c,d\right)=b\times c\\\end{aligned}}}$

Per tant si es vol que les parelles de nombres funcionin tal com intuïtivament es pretén cal identificar amb un mateix nombre totes les parelles que compleixin aquesta igualtat:

${\displaystyle d\times a=b\times c}$

que és exactament el que s'ha fet en definir les classes d'equivalència.

Els nombres enters s'assimilen com un subconjunt dins del conjunt dels nombres racionals a base d'identificar cada nombre enter e amb el nombre racional (e,1).

Notació

Els nombre racionals es poden representar de diferents formes; les més comunes són les fraccions irreduïbles i les representacions decimals, però també es poden representar en altres bases diferents de la base 10 i emprant altres fraccions com les fraccions egípcies.

Fraccions

Els nombres racionals no enters normalment es noten com a fraccions:

${\displaystyle {\frac {a}{b}}}$, on b ha de ser diferent de zero. a s'anomena el numerador, i b el denominador.

Cada nombre racional es pot escriure en una infinitat de fraccions diferents, com ara ${\displaystyle {\frac {3}{6}}={\frac {2}{4}}={\frac {1}{2}}}$, però es diu que està expressat en la seva forma més senzilla o que està expressat amb la seva fracció irreduïble quan a i b no tenen cap divisor comú excepte l'1 (és a dir són coprimers). Tot nombre racional diferent de zero té una i només una expressió en fracció irreduïble amb denominador positiu.

Representació decimal

La representació decimal d'un nombre és una extensió de la representació posicional en base 10 a base de fer servir fraccions on els denominadors són múltiples de 10. Per exemple:

${\displaystyle 112,35=1\times 10^{2}+1\times 10^{1}+2+3{\frac {1}{10}}+5\times {\frac {1}{10^{2}}}}$

Per indicar que un nombre en representació decimal té unes xifres decimals que es repeteixen indefinidament s'escriu una ratlla al damunt de les xifres que es repeteixen. Per exemple:

${\displaystyle 1,0{\overline {142857}}}$

vol dir:

${\displaystyle 1,0142857142857142857...\,}$

Equivalència entre la representació decimal i la representació amb fraccions

Tot nombre racional admet una representació decimal on a partir d'una determinada xifra hi ha un conjunt de xifres decimals, anomenat període, que es repeteix indefinidament. En alguns casos particulars el període es compon d'una única xifra i de vegades aquesta xifra és el zero (llavors es diu que el nombre admet una representació decimal exacta). De vegades el període comença amb la primera xifra decimal llavor es diu que la representació decimal és periòdica pura altrament es diu que és una representació periòdica mixta.

Exemples:

${\displaystyle {\frac {1}{7}}=0,142857\,142857\,142857...}$ (representació decimal periòdica pura amb un període de 6 xifres)

${\displaystyle {\frac {1}{60}}=0,01\,6\,6\,6\,6\,6\,6\,6...}$ (representació decimal periòdica mixta amb un període de 1 xifra)

${\displaystyle {\frac {7}{5}}=1,6}$ (representació decimal exacta 1,6 =1,6000...)

Demostració En efecte, en dividir un enter per un altre, (p. ex. 1 per 7) només existeixen un nombre finit de restes possibles (a l'exemple: 0,1,2,4,8,5,7). Essent la successió de restes infinita, apareixerà forçosament una mateixa resta en dues posicions diferents. A partir d'elles, el càlcul es repeteix indefinidament reproduint sempre la mateixa subsuccessió de residus i de xifres del quocient.

1.................|7

1 0.............. | 0,142857 1...

..30

....20

......60

........40

..........50

............10

(En negreta, les posicions que corresponen al mateix càlcul).

Demostració del reciproc Recíprocament, tot nombre amb un desenvolupament decimal finit o periòdic correspon a un racional. Exemple: Sigui a = 12,345 67 67 67 67 67 ...

Es repeteixen dues xifres; multipliquem a per 10² = 100.

100a = 1234, 567 67 67 67 67 ...

.....a = 12, 345 67 67 67 67 ...

En sostreure, se'n va tota la part periòdica:

100a - a = 1222,22 llavors a = 12222/9900.

Fraccions egípcies

Una Fracció egípcia és una suma d'inverses de nombre naturals.

Tot nombre racional positiu es pot expressar com fracció egípcia (de fet hi ha infinites fraccions egípcies que poden expressar el mateix nombre). Per exemple:

${\displaystyle {\frac {5}{7}}={\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{21}}.}$

Numeració posicional en bases diferents de 10

La representació decimal dels nombres racionals no és res més que un cas particular quant la base és deu, en general en qualsevol base b es poden representar tots els nombres racionals amb la convenció de què a la dreta de la coma les xifres estan multiplicant una fracció amb numerador 1 i denominador la base elevada a un exponent que va creixent una unitat per cada posició,

per exemple, en base 6:

${\displaystyle 123,15=1\times 6^{3}+2\times 6^{2}+3\times 6+1\times {\frac {1}{6}}+5\times {\frac {1}{6^{2}}}}$

Seguint els mateixos raonaments que en base 10, en qualsevol base b els nombres racionals tenen una expressió amb un nombre de xifres a la dreta de la coma que arriba un punt on apareix un període que es repeteix indefinidament. Igual que en base 10 aquest període pot estar format exclusivament per la xifra 0 i llavors es diu que el nombre en aquesta base té una representació exacta. Els nombres que tenen una representació exacta en una base no la tenen en totes les altres, per exemple:

En base 3 ${\displaystyle {\frac {1}{3}}=0,1}$

Però en base 10 ${\displaystyle {\frac {1}{3}}=0,{\overline {3}}}$

Fraccions mixtes

Cada nombre racional ${\displaystyle {\frac {p}{q}}}$ es pot expressar de forma única com ${\displaystyle u\left(A+{\frac {a}{b}}\right)}$ on

• A és un enter no negatiu, és a dir ${\displaystyle A\in \mathbb {Z} ,~A\geq 0}$
• ${\displaystyle {\frac {a}{b}}}$ és una fracció irreduïble no negativa menor que 1. És a dir: ${\displaystyle \mathrm {mcd} \left(a,b\right)=1,\quad 0\leq a<b}$
• ${\displaystyle u}$ és una unitat amb signe. És a dir ${\displaystyle u=\pm 1}$

Les regles per notar-los així són

• ${\displaystyle A{\frac {a}{b}}}$ denota ${\displaystyle A+{\frac {a}{b}}}$
• ${\displaystyle -A{\frac {a}{b}}}$ denota ${\displaystyle -A-{\frac {a}{b}}}$

Per exemple ${\displaystyle -25{\frac {5}{7}}=-{\frac {180}{7}}}$

Operacions aritmètiques amb nombres racionals

Suma

La suma de dues fraccions es defineix amb la següent igualtat:^[4]

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}}$

Aquesta definició es pot acceptar com a tal o es pot interpretar intuïtivament. Si es pretén interpretar el nombre racional a/b com una quantitat que resulta de partir una unitat en b parts iguals i agafar-ne a, llavors si dues fraccions tenen el mateix denominador (la unitat s'ha partit en el mateix nombre de parts iguals) la forma natural de sumar-les (de trobar una fracció que representi una quantitat equivalent a la unió de les quantitats que representaven cada una de les fraccions que es vol sumar) és sumant els numeradors i mantenint el mateix denominador.

En cas de fraccions amb diferent denominador, qualsevol mètode que permeti trobar fraccions equivalents a les originals però que tinguin el mateix denominador permetrà aplicar el criteri que s'ha explicat abans per a fraccions amb el mateix denominador.

En multiplicar el numerador i el denominador d'una fracció per un mateix nombre n s'obté una altra fracció equivalent a la primera (que representa el mateix nombre racional). Això es pot veure acudint a la definició de fraccions o simplement de forma intuïtiva veient que si la unitat es parteix entre un nombre de parts que és el doble o el triple o n cops el denominador inicial però al mateix temps s'agafa el doble o el triple o n cops el numerador inicial, al final es té la mateixa quantitat.

Acudint a la definició de fraccions equivalents:

${\displaystyle anb=bna\Rightarrow {\frac {a}{b}}={\frac {na}{nb}}}$

Això dona diversos mètodes per obtenir faccions amb el mateix denominador però el més senzill d'explicar és multiplicar el numerador i el denominador de la primera fracció pel denominador de la segona i multiplicar el numerador i el denominador de la segona pel denominador de la primera:

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {da}{db}}+{\frac {bc}{bd}}={\frac {ad+bc}{bd}}}$

Que és l'expressió que s'ha fet servir per definir la suma i que coincideix amb el que intuïtivament s'espera. Per què si dos nombres racionals representen una determinada quantitat de matèria el nombre racional resultat de sumar-los representa la unió de les dues quantitats de matèria.

Exemple:

${\displaystyle {\frac {2}{7}}+{\frac {3}{5}}={\frac {2\times 5+7\times 3}{7\times 5}}={\frac {10+21}{35}}={\frac {31}{35}}}$

Si inicialment els denominadors ja són els mateixos també es pot aplicar la definició però és més pràctic sumar els numeradors i conservar el mateix denominador, per veure que els resultat és el mateix fixeu-vos que:

${\displaystyle {\frac {a}{b}}+{\frac {c}{b}}={\frac {ab+bc}{bb}}={\frac {b\left(a+c\right)}{bb}}={\frac {a+c}{b}}}$

Multiplicació

La multiplicació es defineix com:

${\displaystyle {\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}}$

Per interpretar aquesta definició, primer fixeu-vos que si es tracta de multiplicar un nombre natural n per un nombre racional, intuïtivament, es tractaria sumar el nombre racional amb si mateix n cops, per tant hauria de ser:

${\displaystyle n\cdot {\frac {a}{b}}={\frac {a}{b}}+{\frac {a}{b}}+\ldots +{\frac {a}{b}}={\frac {a+a+\ldots +a}{b}}={\frac {na}{b}}}$

El que no és tan immediat d'interpretar és al multiplicar-lo per un nombre fraccionari, per exemple 1/n. Quin sentit pot tenir sumar un nombre amb si mateix 1/n cops? La idea per donar sentit a aquest concepte consisteix en buscar la solució que permeti mantenir la propietat associativa, si es vol que:

${\displaystyle \left({\frac {n}{1}}\cdot {\frac {1}{n}}\right)\cdot {\frac {a}{b}}={\frac {n}{1}}\cdot \left({\frac {1}{n}}\cdot {\frac {a}{b}}\right)}$

S'ha de definir ${\displaystyle {\frac {1}{n}}\cdot {\frac {a}{b}}}$ de forma que ${\displaystyle {\frac {n}{1}}\cdot \left({\frac {1}{n}}\cdot {\frac {a}{b}}\right)={\frac {a}{b}}}$ perquè ${\displaystyle 1=\left({\frac {n}{1}}\cdot {\frac {1}{n}}\right)}$ per tant cal definir:

${\displaystyle {\frac {1}{n}}\cdot {\frac {a}{b}}={\frac {a}{n\cdot b}}}$. (perquè ${\displaystyle {\frac {n}{1}}\cdot {\frac {a}{n\cdot b}}={\frac {n\cdot a}{n\cdot b}}={\frac {a}{b}}}$)

I per tant:

${\displaystyle {\frac {a}{b}}\cdot {\frac {c}{d}}=\left({\frac {a}{1}}\cdot {\frac {1}{b}}\right)\cdot {\frac {c}{d}}={\frac {a}{1}}\cdot \left({\frac {1}{b}}\cdot {\frac {c}{d}}\right)={\frac {a}{1}}\cdot {\frac {c}{b\cdot d}}={\frac {a\cdot c}{b\cdot d}}}$

Que és tal com s'ha definit la multiplicació de nombres racionals. Per exemple:

${\displaystyle {\frac {2}{5}}\cdot {\frac {3}{7}}={\frac {2\cdot 3}{5\cdot 7}}={\frac {6}{35}}}$

Resta

L'element oposar d'una fracció es defineix com:

${\displaystyle -\left({\frac {a}{b}}\right)={\frac {-a}{b}}={\frac {a}{-b}}}$

Cal que la definició es faci d'aquesta manera perquè la suma de qualsevol racional amb el seu oposat doni zero:

${\displaystyle {\frac {a}{b}}+\left[-\left({\frac {a}{b}}\right)\right]={\frac {a}{b}}+{\frac {-a}{b}}={\frac {a-a}{b}}={\frac {0}{b}}={\frac {0}{1}}=0}$

Llavors es defineix la resta de forma habitual com la suma amb l'element oposat:

${\displaystyle {\frac {a}{b}}-\left({\frac {c}{d}}\right)={\frac {a}{b}}+{\frac {-c}{d}}={\frac {ad-cb}{bd}}}$

Exemple:

${\displaystyle {\frac {7}{3}}-{\frac {6}{5}}={\frac {7\times 5-6\times 3}{3\times 5}}={\frac {35-18}{15}}={\frac {17}{15}}}$

Divisió

L'element invers es defineix com:

${\displaystyle \left({\frac {a}{b}}\right)^{-1}={\frac {b}{a}}{\mbox{ si }}a\neq 0}$

Com en el cas anterior la definició cal fer-la així perquè el producte d'un element pel seu invers doni 1:

${\displaystyle {\frac {a}{b}}\cdot \left({\frac {a}{b}}\right)^{-1}={\frac {a}{b}}\cdot {\frac {b}{a}}={\frac {ab}{ba}}=1}$

S'ha de prohibir l'invers d'una fracció amb zero al numerador perquè al seguir la regla quedaria una fracció amb zero al denominador que al definir els nombres racionals es va haver de prohibir.

Llavors la divisió es defineix de forma habitual com el producte per l'element invers:^[5]

${\displaystyle {\frac {a}{b}}\div {\frac {c}{d}}={\frac {ad}{bc}}}$

Exemple:

${\displaystyle {\frac {7}{3}}\div {\frac {6}{5}}={\frac {7\times 5}{3\times 6}}={\frac {35}{18}}}$

Trobar la fracció irreduïble

Si en una fracció es divideix el numerador i el denominador per un mateix nombre la fracció que en resulta és equivalent a la inicial, això es pot comprovar com segueix:

${\displaystyle a\cdot \left(b\div c\right)=\left(a\cdot b\right)\div c=b\cdot \left(a\div c\right)\Rightarrow {\frac {a}{b}}={\frac {a\div c}{b\div c}}}$

Per tant si es divideix el numerador i el denominador de forma que el resultat no tinguin cap divisor comú s'haurà trobat la fracció irreduïble (vegeu definició de fracció irreduïble). Llavors el problema de trobar la fracció irreduïble es resol fent:

1. Trobar el màxim comú divisor entre el numerador a i el denominador b.
2. Dividir a i b entre el Mcd que s'ha trobat obtenint a' i b' .
3. La fracció irreduïble és la que té per numerador a' i denominador b' .

Per trobar el màxim comú divisor de dos nombres enters es poden descompondre en factors primers i el Mcd és el nombre que té tots els factors comuns elevats al mínim exponent. Per nombres grans aquest mètode és molt ineficient, l'algorisme d'Euclides permet obtenir-lo molt més ràpidament. L'algorisme d'Euclides es basa en el fet que si un nombre c és divisor comú d'altres dos a i b també ho és de a' i b' on a' és el divisor de la divisió euclidiana de a entre b (és a dir a' = b) i b' n'és el residu (divisió euclidiana és la divisió sense trobar decimals i trobant el residu). Per tant per trobar el Mcd de dos nombres es divideix el més gran entre el més petit si el residu és zero el Mcd és el més petit si no es repeteix el procés amb el quocient i el residu.

Si es treballa amb fraccions irreduïbles, després de cada operació cal trobar la fracció irreduïble del resultat perquè no sempre el resultat d'una operació amb fraccions irreduïble és una fracció irreduïble. Per exemple 1/2 + 1/2 = 2/2 que és reductible a 1.

Exemple descomponent en factors primers

Trobar la fracció irreduïble de ${\displaystyle {\frac {31.360}{82.467}}}$

Emprant els criteris de divisibilitat es pot veure que 31.360:

• és divisible entre 2 perquè acaba en zero que és múltiple de 2
• és divisible entre 5 perquè acaba en 0 que és múltiple de 5
• és divisible entre 7 perquè 360-31=329 que és múltiple de 7 perquè: 32-2*9=14 que és múltiple de 7

Dividint entre aquests nombres (repetidament quant el resultat encara és divisible) entre el nombre resulta que:

${\displaystyle 31.360=2^{7}\cdot 5\cdot 7^{2}}$

I 82.467:

• és divisible entre 3 perquè 8+2+4+6+7=27 que és divisible entre 3 perquè 2+7=9 que és múltiple de 3
• és divisible entre 7 perquè 467-82=385 que és múltiple de 7 perquè 38-2*5=28 que és múltiple de 7 (28=4*7)
• és divisible entre 11 perquè 8-2+4-6+7=11 que és múltiple de 11
• és múltiple de 17 perquè 8.246-5*7=8.211; 821-5*1=816; 81-5*6=51; 5-5*1=0 que és múltiple de 17.

Dividint entre aquests nombres (repetidament quant el resultat encara és divisible) entre el nombre resulta que:

${\displaystyle 82.467=3^{2}\cdot 7^{2}\cdot 11\cdot 17}$

Per tant el Mcd és 7²

Llavors la fracció irreduïble resulta:

${\displaystyle {\frac {31.360}{82.467}}={\frac {2^{7}\cdot 5\cdot 7^{2}}{3^{2}\cdot 7^{2}\cdot 11\cdot 17}}={\frac {2^{7}\cdot 5}{3^{2}\cdot 11\cdot 17}}={\frac {640}{1683}}}$

A banda de les operacions necessàries per verificar els criteris de divisibilitat s'han hagut de fer 14 divisions i al final multiplicar els factors per trobar el resultat final.

Exemple amb l'algorisme d'Euclides

82.467 | 31.360
-------------- 
-62.720 2
-------
19.747

31.360 | 19.747
-------------- 
-19.747 1
-------
11.613

19.747 | 11.613
-------------- 
-11.613 1
-------
8.134

11.613 | 8.134
-------------- 
-8.134 1
-------
3.479

8.134 | 3.479
-------------- 
-6.958 2
-------
1.176

3.479 | 1.176
-------------- 
-2.352 2
-------
1.127

1.176 | 1.127
-------------- 
-1.127 1
-------
49

1.127 | 49
-------------- 
-1.027 23
-------
0

Per tant el Mcd és 49 i quan es divideix numerador i denominador entre 49 s'obté:

${\displaystyle {\frac {31.360\div 49}{82.467\div 49}}={\frac {640}{1.683}}}$

En aquest cas amb 8 divisions n'hi ha hagut prou per trobar el Mcd i després dues divisions més per trobar el resultat final.

Relació d'ordre

En el conjunt dels nombres racionals es defineix una relació d'ordre de la següent manera:

Si a i b són dos nombres racionals es diu que ${\displaystyle a\geq b}$ (i es llegeix a és més gran o igual que b) si i només si ${\displaystyle a-b}$ és no negatiu.

Exemple:

${\displaystyle {\frac {5}{11}}-{\frac {3}{7}}={\frac {5\times 7-3\times 11}{11\times 7}}={\frac {35-33}{77}}={\frac {2}{77}}\Rightarrow {\frac {5}{11}}\geq {\frac {3}{7}}}$

Es compleix que aquesta relació d'ordre és total perquè ${\displaystyle a-b=-(b-a)}$ i també es compleix que si a ≥ b i b ≥ a ha de ser a = b perquè ha de ser a - b =0.

Propietats

• Els nombres racionals compleixen la propietat de la densitat. Això vol dir que per a qualsevol parella de nombres racionals existeix algun altre nombre racional situat entre els dos a la recta real (${\displaystyle \mathbb {R} }$).

• A més, ${\displaystyle \mathbb {Q} }$ és dens a ${\displaystyle \mathbb {R} }$, o sigui que entre dos reals diferents, sempre cap un racional.

demostració

Aquesta propietat és conseqüència de l'arquimedianitat de ${\displaystyle \mathbb {R} }$.

Siguin dos reals diferents. ${\displaystyle a\,}$ i ${\displaystyle b\,}$ on el més petit és ${\displaystyle a\,}$ i el més gran ${\displaystyle b\,}$.

Cal veure que existeix un racional entre els dos.

Sigui ${\displaystyle d\,}$ el real estrictament positiu ${\displaystyle b-a\,}$. En ser ${\displaystyle \mathbb {R} }$ arquimedià, existeix un enter ${\displaystyle q\,}$ tal que ${\displaystyle 1/d<q\,}$.

Es considera llavors el conjunt dels enters ${\displaystyle p\,}$ tals que ${\displaystyle {\frac {p}{q}}\leq a}$. Com que ${\displaystyle \mathbb {R} }$ és arquimedià, aquest conjunt no és buit i està fitat superiorment. Admet per tant un suprem ${\displaystyle p_{0}\,}$ tal que :${\displaystyle {\frac {p_{0}}{q}}\leq a<{\frac {p_{0}}{q}}+{\frac {1}{q}}<b}$.

El nombre racional ${\displaystyle {\frac {p_{0}+1}{q}}}$ està estrictament comprès entre ${\displaystyle a\,}$ i ${\displaystyle b\,}$.

• Es pot demostrar amb facilitat que el cardinal dels nombres racionals és el mateix que el dels enters, el que significa que no hi ha més racionals que enters. A la figura de la dreta es presenta una forma d'ordenar el nombres racionals i comptar-los de manera que tard o d'hora qualsevol nombre racional serà comptat.

• Un nombre és racional si i només si el seu desenvolupament en fracció contínua és finit. Aquesta propietat és la base per a la demostració de la irracionalitat del Nombre e i de π.

Propietats de la suma i la multiplicació

• La suma en Q és commutativa: ${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={\frac {c}{d}}+{\frac {a}{b}}}$
• La suma en Q és associativa: ${\displaystyle {\frac {a}{b}}+\left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}+{\frac {c}{d}}\right)+{\frac {p}{q}}=\left({\frac {a}{b}}+{\frac {p}{q}}\right)+{\frac {c}{d}}}$
• La multiplicació en Q és associativa: ${\displaystyle {\frac {a}{b}}\times \left({\frac {c}{d}}\times {\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)\times {\frac {p}{q}}}$
• La multiplicació té la propietat distributiva respecte de la suma: ${\displaystyle {\frac {a}{b}}\times \left({\frac {c}{d}}+{\frac {p}{q}}\right)=\left({\frac {a}{b}}\times {\frac {c}{d}}\right)+\left({\frac {a}{b}}\times {\frac {p}{q}}\right)}$

Totes aquestes propietats són conseqüència directa de les mateixes propietats en els nombres enters i es demostren directament aplicant les definicions de suma i multiplicació i després les propietats corresponents en els nombres enters.

Generalització

La definició formal dels nombres racionals es pot fer servir per generalitzar el concepte de nombres racionals aplicant-la a cossos diferents del cos dels nombres naturals. Llavors es parla del cos de les fraccions.

Per exemple si s'aplica al cos dels polinomis llavors es construeix el cos de les fraccions racionals.

Notes i referències

Vegeu també

• Coma flotant
• Nombre racional de Gauss